Array Коллектив авторов - Инновационные и приоритетные направления в преподавании гуманитарных дисциплин в техническом вузе. Сборник трудов по материалам III Международной научно-практической конференции 21 апреля 2016 г.

Работая над развитием устной математической речи, часто требуется помогать студентам, корректно поставить вопрос. Правильно сформулированный и в нужное время заданный вопрос помогает обучаемому излагать свои мысли с большей точностью, логично строить рассуждения, употреблять только нужные слова и этим достигать необходимой краткости. Именно на занятиях по математике (лекциях и практических занятиях) студенты должны привыкать к краткой, четкой, логически обоснованной речи. Математика приучает к тому, что даже в обычной речи человек будет стараться избегать слов и фраз, которые не несут смысловой нагрузки [1]. В этом помогает использование на занятиях по математике кванторов (квантор существования и квантор всеобщности) и знакомство с символьным языком доказательств.

Большое значение имению понимать и различать выражения русского языка такие, как «по крайней мере, со второго раза», «хотя бы три», «не более трех», «по крайней мере три», требуется при изучении комбинаторики и теории вероятностей. Язык этого раздела значительно отличается от языка других математических дисциплин. Полезно к каждому типу задач составлять перечень вопросов, логически подводящих к нахождению решения. И то, что при оформлении решении почти каждой задачи требуется сформулировать и описать такие понятия, как «испытание», «событие», а также в определенных задачах составить еще и «гипотезы», формирует как уровень владения математическим языком, так и уровень понимания изучаемого материала.

Пример.В ящике находятся детали первого, второго и третьего сорта. Наудачу извлекается одна деталь. Событие А – деталь первого сорта. Событие В – деталь второго сорта. Событие С – деталь третьего сорта. Сформулируйте, что представляет собой событие: А+В,, АС, АВ+С.

Решение.Событие: А+В означает, что вынута деталь первого или второго сорта.

Событие:, то есть вынута деталь второго сорта, так как событие А+С означает, что деталь первого или третьего сорта. Событие: АС – невозможное, так как деталь не может быть одновременно и первого и третьего сорта. Событие: АВ+С – это сумма невозможного АВ и С, то есть деталь третьего сорта.

Таким образом, развитие математической речи в курсе теории вероятностей – это очередной этап учебно-исследовательской деятельности по формированию у студентов математически верной устной и письменной речи. В математическом языке выделяет два компонента: язык данной математической теории (каждый раздел математики пользуется своим особым языком) и логический язык, состоящий из терминов и символов, обозначающих логические операции, используемые для конструирования предложений и для вывода одних предложений из других [2].

Формированию культуры математической речи может способствовать специально разработанная система задач, в которую целесообразно включать следующие задания [2]:

Задания для работы с терминологией, символикой и графическими изображениями.

Задания для работы со словесно-логическими конструкциями математического языка.

Задания для работы с письменными обучающими текстами по математике.

Виды математической речи можно представить в виде следующей таблицы, где для каждого вида сформулированы конкретные приемы для их развития (рис.1).

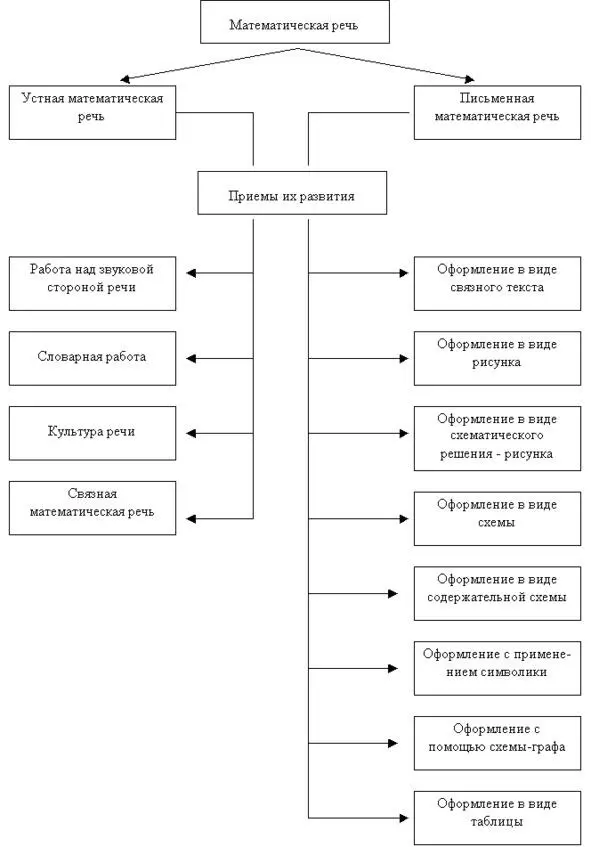
Рисунок 1

Рассмотрим простейшие примеры приемов развития устной математической речи.

Работа над звуковой стороной речиозначает формирование правильного произношения и выразительного чтения математических терминов и любого задания. Для успешного решения этой задачи студентам надо следить, прежде всего, за речью преподавателя.

Словарная работана занятиях математики сводится к пониманию и умению объяснять значение математических терминов, усвоению их правильного написания и формированию умений составлять содержательное связное высказывание. С этой целью полезно выполнить упражнения следующих видов:

1) упражнения на объяснение значений математических терминов (объясните значение слов и выражений: функция, аргумент, дифференциал, экспонента);

2) упражнения на составление правильных связных высказываний (прочитайте предложения, вставив пропущенные слова: « С геометрической точки зрения производная …, вычисленная… равна… касательной, проведенной к… функции в точке, с…» .