Константин Суриков - Человек в космосе мышления. Введение в эпистемологию (сборник)

Спрашивается, какова мощность каждой из моделей развития самоосознания человека? Сравнить мощность этих моделей можно, построив общее семантическое поле. Здесь нам поможет математика, которая, в отличие от физики, никогда не имела проблем с теологией.

Круг – это периметр, ограничивающий наибольшую площадь. То есть это фигура, отличающаяся наибольшей, говоря аллегорически, «площадной» мощностью по сравнению с другими фигурами того же периметра. Проанализируем, каким образом совершается этот прирост площади, с двух разных стартовых позиций: окружности и треугольника.

Пойдем сначала извне вовнутрь, от окружности к диаметру.

Круг мы определяем как периметр, ограничивающий наибольшую площадь. Если теперь мы впишем в круг правильный шестиугольник, то сторона такого шестиугольника всегда будет равна радиусу (рис. 1).

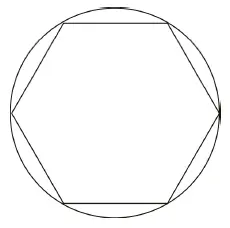
рис. 1.

В качестве отправной точки размышлений возьмем число «пи» в его дробном выражении, знакомом еще Архимеду и дающем приближение до трех цифр: π = 22: 7 = 3,14. Поскольку π – это длина окружности, деленная на два радиуса (L: 2R), то, если мы будем считать числовым значением длины окружности 22, длина радиуса равна: диаметр, деленный на два: 7: 2 = 3,5. Посчитаем теперь периметр шестиугольника: он равен значению радиуса, умноженному на шесть. Итак – 3,5 × 6 = 21, число Больших Арканов без Шута (Дурака, нулевого Аркана). Далее: длина окружности равна 22, отнимем от нее периметр шестиугольника 21, получим 1. Это Δφ («дельта фи") – та разница, которая дает прирост площади круга (Дурак в некоторых толкованиях – это новизна, например новый путь в жизни человека).

Теперь пойдем изнутри наружу, от гипотенузы прямоугольного треугольника (диаметра) к окружности. Посчитаем сначала длину окружности по формуле: L = 2πR, взяв за единицу измерения радиус: R = 1, тогда L = 2π × 1 = 2 × 3,14 = 6,28. Теперь, исходя из той же логики, посчитаем периметр шестиугольника, вписанного в круг, в этом случае он равен: 1 × 6 =6. А теперь посчитаем Δφ («дельту фи»). Для этого отнимем: 6,28 -6 = 0,28. Теперь мы получили выражение прироста площади в другой модели. Чтобы сравнить эти величины, воспользуемся понятием Δφ как «площадной мощностью» по аналогии с мощностью тока, которая есть прохождение «количества» тока через площадь сечения в единицу времени.

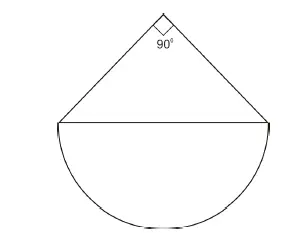
рис. 2.

Чтобы сделать сравнение по предложенному параметру мощности прироста пощади, рассмотрим окружность и треугольник одновременно, буквально в одну и ту же секунду, так как мощность – это сила в единицу времени. Как это можно сделать в восприятии человека? Для этого совместим окружность и треугольник в визуальном поле человека, то есть в данном случае – на плоскости. В результате совмещения по линии диаметра (гипотенузы) мы получаем фигуру, состоящую из треугольника, опирающегося на дугу в сто восемьдесят градусов (рис. 2). Δφ, полученная в результате пути от окружности к диаметру, равна 1, соответственно, в данной совмещенной модели она будет равна 0,5, так как мы имеем теперь не окружность, а ее половину. Δφ, образовавшаяся благодаря движению от диаметра к окружности, равна по-прежнему 0,28, потому что треугольник при совмещении остался целым. Теперь, если рассматривать две модели одновременно, то есть в одну и ту же секунду, то это значит, как бы рассматривать их с точки зрения мощности. На самом деле это аллегория мощности, так как площадь, рассматриваемая в секунду, – это условность. То есть мы рассматриваем их в одну и ту же секунду, и тогда мы как бы получаем величину прироста площади

– как бы мощность. И эта аллегория нам показывает, что «дельту фи» треугольника осталась целой, тогда как «дельту фи» окружности уменьшилась вполовину. Таким образом, становится ясно, что модель треугольника более мощная, точнее, она мощнее модели окружности ровно в два раза.

Для дальнейших рассуждений мы должны с целью восстановления целостности выровнять «дельта фи» путем умножения на 2, так как в природе не существует половинок. Поэтому мы будем умножать 0,5 на два и получим 1. Потом мы, следуя логике, должны умножить 0,28 на 2 и в результате получить 0,56. Число, стоящее после запятой, – 56 – количество Малых Арканов в колоде Таро. Мы начали наши рассуждения с 22 Больших Арканов и пришли к 56 Малым Арканам, которые символизируют собой бесконечные возможности или принцип многообразия.