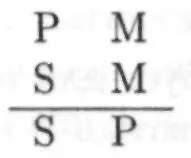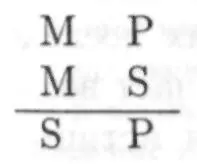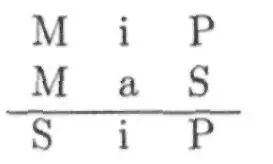Хаймо Хофмайстер - Что значит мыслить философски [Поиск фундамента всего знания и всего сущего]

Начальные буквы ключевых слов, не принадлежащих к первой фигуре заключения, сообщают при этом, каким заключением первой фигуры может быть доказано значение.

Ключевые слова восходят к Петру Испанскому [312]и сформулированы гекзаметром:

I. Barbara, Celarent primae, Darii, Ferioque.

II. Cesare, Caemstrens, Festino, Baroco secundae.

III. Tertia grande sonans recital Darapti, Felapton, Disamis, Datisi, Bocardo, Ferison.

IV. Quartae sunt Bamalip, Calemes, Dimatis, Fesaro, Fresison.

Рассмотрим теперь фигуры заключения, чтобы попутно дать примеры преобразования.

I. Фигура:

В этой фигуре можно сделать выводы согласно логическому квадрату в следующих комбинациях: ааа, eae, aii, eio.

Примером для фигуры заключения Barbara (ааа) будет:

Все люди смертны.

Все афиняне — люди.

Следовательно, все афиняне смертны.

II. Фигура:

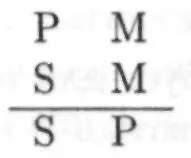
Для этой фигуры заключения возможны в следующих комбинациях: eae, aee, eio, аоо.

Примером для фигуры заключения Caemstres (aee) будет:

Все лошади — непарнокопытные.

Ни один вол не является непарнокопытным.

Следовательно, ни один вол не является лошадью.

III. Фигура:

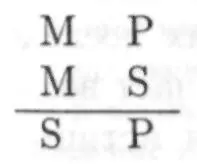
Здесь возможны следующие фигуры заключения: aai, aii, еао, eio, iai, оао.

Примером для фигуры заключения Darapti (aai) будет:

Все скрипки — смычковые инструменты.

Все скрипки — музыкальные инструменты.

Следовательно, некоторые музыкальные инструменты являются смычковыми инструментами.

IV. Фигура:

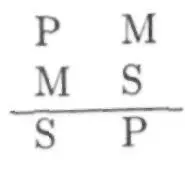
В этой фигуре могут быть получены заключения в соответствии со следующими комбинациями: aai, aee, iai, еао, eio. Примером для фигуры заключения Bamalip (aai) будет:

Все афиняне — люди.

Все люди смертны.

Следовательно, некоторые смертные — афиняне.

II, III и IV фигуры заключения сводимы к I фигуре заключения и правило, которому здесь нужно следовать, называется соответствующим ключевым словом. Возьмем пример: модус Disamis (iai) III фигуры заключения нужно преобразовать в модус I фигуры. Начальная буква D указывает на то, что модус Disamis следует свести к модусу Darii (aii) первой фигуры заключения. Модус Darii имеет следующий вид:

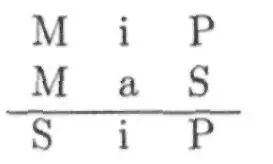
S в ключевом слове Disamis в соответствии с i требует для первой посылки conversio simplex, т. е. ее следует преобразовать в Ρ i Μ. Μ показывает, что нужно предпринять перестановку посылок. Прежнее преобразование дало бы в качестве вывода Ρ i S. Последняя буква в названии Disamis, s, указывает на то, что также нужно предпринять conversio simplex этого вывода, так что в качестве результата получится: S i Р. Тем самым мы получили силлогизм первой фигуры.

Логика не является теорией истины [313]и не стремится ею быть. С отказом от знания содержания и ограничением своих исследований формой понятий, суждений и заключений она получает возможность позитивно говорить об истине. Для определения истины последовательность суждений и заключений может быть conditio sine qua поп, хотя истина не производится и не устанавливается логикой.

Ответ на вопрос Пилата «Что есть истина?» в истории западной философии давали Платон и Аристотель, а классическую формулировку он получил у Фомы Аквинского:

Veritas est adaequatio rei et intellectus. [314]

Утверждение истины как соответствия, корреспонденции мышления и бытия под названием «теории корреспонденции» наряду с так называемой «теорией когерентности» была самой значительной попыткой определения истины. Когерентное понимание истины стало рассматриваться иначе, чем корреспондентное, прежде всего в мышлении Нового времени, а истина стала пониматься как универсальная связь предложений [315]и их формальное и содержательное соответствие друг другу.

Сформулированная в теории корреспондентности и когерентности проблематика постижения того, что мы обозначаем познавательной истиной, лежит в основе всех других теорий истины, в том числе и прагматической. Обе только что названные теории опираются на то понимание истины, которое интерпретирует истину не только как высказанную истину, но и полагает истину в смысле соответствия идеи и явления, понятия и сущего. Вследствие этого и возможно называть истинными нормы, поступки, словесные выражения, вещи и личности.