Борис Шулицкий - Мадэализм — концепция мировоззрения III тысячелетия (заметки по поводу модернизации физической теории)

Интересно заметить, что в последовательности возникновения основных разделов математики проявляется закон отрицания отрицания (9,70) (см. схему).

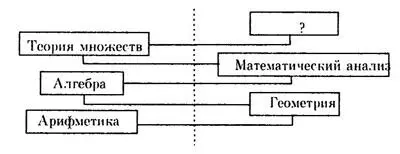
«Так, — пишет Н.И. Жуков, — создание системы символов для обозначения переменных величин в алгебре (работы Ф. Виета), введение буквенного коэффициента в уравнения представляет собой как бы возврат к арифметике, но на новой основе. В свою очередь, возникновение математического анализа есть не что иное, как распространение понятия переменной величины из области дискретного на область непрерывного с последующим освобождением функций от их геометрической интерпретации. Наконец, появление теоретико-множественного подхода определило перенесение центра тяжести снова на область дискретного» (9,70). Таким образом, следующий раздел математики должен перенести центр тяжести опять в область непрерывного, то есть исходить из теории множеств и иметь какие-то аналогии с разделом исчисления бесконечно малых. На наш взгляд, таким разделом может стать детерминальное исчисление.

Математической дисциплиной, наиболее близко подошедшей к осознанию необходимости символьного отражения диалектического характера процессов изменения, развития, является математическая логика. «Идея логического исчисления высказываний, суждений содержалась еще в трудах Лейбница (в работе „Искусство комбинаторики“, например). Однако основы математической логики удалось заложить лишь в XIX веке Дж. Булю, который создал алгебру логики. Впрочем, его работы современниками всерьез не принимались и многими, даже видными, учеными рассматривались как простой курьез, плод досужего ума, в лучшем случае. Одновременно основы новой науки успешно разрабатывал А. Морган, но главным образом — Э. Шредер, так что начиная с конца XIX века она стала называться алгеброй Буля — Шредера. Большой вклад в ее дальнейшее развитие внесли П.С. Порецкий, Фреге, Пеано и, конечно же, известный философ Рассел, который совместно с А. Уайтхедом в начале XX века создал капитальный труд „Принципы математики“. Именно с Фреге и Рассела начинается новый этап в развитии логики как исчисления. С середины XX века она получила особенно большое развитие в связи с успехами кибернетики и информатики и является ныне важнейшей областью математического знания» (9,59).

«В основе математической логики лежит исчисление высказываний и предикатов, в котором суждения обозначаются знаками, с которыми впоследствии можно оперировать как с обычными математическими символами. В кибернетике и информатике идут еще дальше: „атомарные“ (далее неразложимые) высказывания обозначают буквами или знаками, а связки, рассматриваемые в качестве логических операторов, моделируют с помощью инверторов, конъюнкторов и дизъюнкторов, что позволяет для последующих исчислений использовать компьютер. Особого внимания заслуживает родство, общность математической логики с теорией множеств. Это обстоятельство дает право говорить о математической логике как об особой области современной математики, смыкающейся с теорией множеств» (9,60—61).

Современная математическая логика есть результат символизации и математизации традиционной логики, так что «и обычная, и математическая логика чаще всего обозначаются одним, более общим термином — „формальная“» (9,56). Она интерпретируется многими «как современный этап развития формальной логики» (9,57). Естественно узнать, почему математическая логика конца XX века базируется на построенной Аристотелем более двух тысячелетий назад формальной логике, игнорируя разработанную Гегелем менее двухсот лет назад диалектическую логику?

«Формальная логика, — пишет Н.И. Жуков, — наука о законах и формах правильного (последовательного и непротиворечивого) мышления. Только следование ее правилам делает рассуждения четкими, ясными и последовательными» (9,55). Но при этом далее уточняет: — «Однако адекватными действительности формами мышления будут те, которые являются предметом диалектической логики, способной выразить реальное противоречие внешнего мира, движение в объективной действительности» (9,56). Еще Ф. Энгельс отмечал, что «именно диалектика является для современного естествознания наиболее важной формой мышления , ибо только она представляет аналог и тем самым метод объяснения для происходящих в природе процессов развития, для всеобщих связей природы, для переходов от одной области исследования к другой» (7,367). Вот почему теория диалектики дает основополагающие принципы познания и преобразования действительности, являясь универсальной методологической, «принципиальной, выверенной основой естественнонаучного и социального познания» (9,55).