Так, немецкий физик, один из основателей термодинамики, Рудольф Клаузиус (1822–1888 гг.), утверждал, что «теплота не может переходить сама собой от более холодного тела к более теплому». Его английский коллега Уильям Томсон (барон Кельвин) сформулировал принцип Карно и дал такое толкование второго начала: «невозможно существование такой тепловой машины, которая производила бы путем охлаждения моря или земли механическую работу в любом количестве, вплоть до исчерпания теплоты суши и моря». (Дополнительные уточнения формулировок и сути второго начала термодинамики сделаем после введения понятия энтропия.)
Обратные процессы, переводящие систему из более вероятного состояния в менее вероятное, самопроизвольно не протекают. Такие процессы могут быть возможны только при определенном, специфически организованном подводе энергии из какого-либо внешнего источника. С такими процессами человек познакомился с изобретением паровой машины — первой машины, для преобразования хаотического движения в организованное — именно, тепла в работу. Как уже упоминалось, Карно доказал, что такое преобразование не может быть полным — часть тепловой энергии обязательно должна быть диссияирована, рассеяна (отдана холодильнику). Отсюда следует еще такой кельвинский вариант формулировки второго начала термодинамики: невозможен процесс, единственным результатом которого было бы поглощение теплоты от нагревателя и полное преобразование этой теплоты в работу.
Итак, второе начало термодинамики позволяет разделить все процессы на естественные — переход работы в тепло, самопроизвольный переток тепла от горячего тела к холодному — и на противоестественные.
Далее мы рассмотрим достаточно сложные в естествознании понятия энтропии, энтальпии, негэнтропии, свободной энергии, характеризующие тепловые или термодинамические процессы, процессы обмена энергией, веществом в больших природных системах, отнеся вопросы энергетики в живых системах в раздел о концепциях и принципах биологического естествознания, (глава 9). Знание таких понятий и процессов необходимы для понимания явлений химического и биологического типов, характеризующихся, практически на всех стадиях своего развития, самоорганизацией и эволюцией. В некоторых случаях мы будем употреблять для иллюстрации формулы, которые нет необходимости запоминать.
Понятие энтропии (от греч. еп — в, внутри + trope — поворот, превращение) как меры внутренней неупорядоченности системы было введено Клаузиусом следующим
образом: 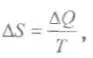 где приращение энтропии системы
где приращение энтропии системы 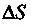 связано с увеличением количества тепла
связано с увеличением количества тепла 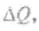 получаемого системой, а сам переход системы из одного состояния в другое происходит обратимым образом, Т — температура системы.
получаемого системой, а сам переход системы из одного состояния в другое происходит обратимым образом, Т — температура системы.
Любой самопроизвольно протекающий в замкнутой изолированной системе процесс должен увеличивать эту величину. Рассмотрим, например, как будет меняться эта величина при выравнивании температур в неравномерно нагретом теле. При этом процессе некоторое количество тепла перейдет от горячей части к холодной — одна часть теряет (рассеивает), а другая приобретает одно и то же количество тепла. Энергия системы не изменится, но горячая часть системы потеряет тепло при большей температуре Т1, чем холодная при температуре Т2 ее приобретет, и, значит, потеря энтропии горячей частью будет меньшей, чем ее увеличение в холодной — энтропия всей системы возрастет: 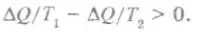
Энтропия кажется, и не без оснований, весьма загадочной и непривычной характеристикой состояния термодинамической системы, но на самом деле она несколько иная характеристика системы, чем энергия, и столь же полноправная. Если энергия — это мера некоторой потенциальной возможности системы совершить полезную работу, то есть упорядоченное действие, то энтропия — это мера качества энергии, то есть реальной способности ее произвести работу без привлечения внешнего воздействия. Энтропия возрастает при рассеянии энергии, при возрастании неупорядоченности системы, при возрастании хаоса.
Статистическое определение энтропии было дано впервые австрийским физиком Людвигом Больцманом (1844–1906 гг.). Он связал энтропию системы с вероятностью макроскопического состояния системы 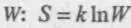 , где k — так называемая постоянная Больцмана, равная отношению универсальной газовой постоянной R к числу Авогадро N A. Величина W представляет собой число способов, которыми можно осуществить (создать, организовать) данную систему, и эта величина определяет вероятность реального ее осуществления (организации). Любая упорядоченность, возникающая в системе, ограничивает число ее возможных конфигураций, уменьшает вероятность ее существования в таком виде и энтропию. Перемешивание, пространственное выравнивание концентраций увеличивает число вариантов взаиморасположений конкретных молекул, обеспечивающих данную конфигурацию, а увеличение температуры или выравнивание ее увеличивает число вариантов распределения энергии между частицами системы (молекулами), обеспечивающих данную среднюю энергию.
, где k — так называемая постоянная Больцмана, равная отношению универсальной газовой постоянной R к числу Авогадро N A. Величина W представляет собой число способов, которыми можно осуществить (создать, организовать) данную систему, и эта величина определяет вероятность реального ее осуществления (организации). Любая упорядоченность, возникающая в системе, ограничивает число ее возможных конфигураций, уменьшает вероятность ее существования в таком виде и энтропию. Перемешивание, пространственное выравнивание концентраций увеличивает число вариантов взаиморасположений конкретных молекул, обеспечивающих данную конфигурацию, а увеличение температуры или выравнивание ее увеличивает число вариантов распределения энергии между частицами системы (молекулами), обеспечивающих данную среднюю энергию.
Читать дальше

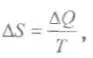 где приращение энтропии системы
где приращение энтропии системы 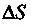 связано с увеличением количества тепла
связано с увеличением количества тепла 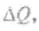 получаемого системой, а сам переход системы из одного состояния в другое происходит обратимым образом, Т — температура системы.
получаемого системой, а сам переход системы из одного состояния в другое происходит обратимым образом, Т — температура системы.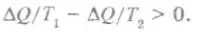
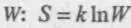 , где k — так называемая постоянная Больцмана, равная отношению универсальной газовой постоянной R к числу Авогадро N A. Величина W представляет собой число способов, которыми можно осуществить (создать, организовать) данную систему, и эта величина определяет вероятность реального ее осуществления (организации). Любая упорядоченность, возникающая в системе, ограничивает число ее возможных конфигураций, уменьшает вероятность ее существования в таком виде и энтропию. Перемешивание, пространственное выравнивание концентраций увеличивает число вариантов взаиморасположений конкретных молекул, обеспечивающих данную конфигурацию, а увеличение температуры или выравнивание ее увеличивает число вариантов распределения энергии между частицами системы (молекулами), обеспечивающих данную среднюю энергию.
, где k — так называемая постоянная Больцмана, равная отношению универсальной газовой постоянной R к числу Авогадро N A. Величина W представляет собой число способов, которыми можно осуществить (создать, организовать) данную систему, и эта величина определяет вероятность реального ее осуществления (организации). Любая упорядоченность, возникающая в системе, ограничивает число ее возможных конфигураций, уменьшает вероятность ее существования в таком виде и энтропию. Перемешивание, пространственное выравнивание концентраций увеличивает число вариантов взаиморасположений конкретных молекул, обеспечивающих данную конфигурацию, а увеличение температуры или выравнивание ее увеличивает число вариантов распределения энергии между частицами системы (молекулами), обеспечивающих данную среднюю энергию.