Георгий Рузавин - Логика и аргументация - Учебн. пособие для вузов.

x ∈ К,

где х - обозначает элемент;

К - класс таких элементов;

символ " ∈ "обозначает принадлежность элемента классу.

Эти соображения лежат в основе современного подхода к силлогистике, при котором рассуждения о свойствах заменяются рассуждениями о классах, а точнее, об объемах понятий классов.

Рассмотрим в этих целях основные отношения между классами, но предварительно введем некоторые новые понятия. Если каждый элемент класса K 1есть одновременно элемент класса К 2, тогда класс K 1есть подкласс класса К 2. Символически: K 1⊂ К 2или К 2 ⊃K 1. Говорят также, что класс K 1входит или включается в класс K 2. Отношение включения обозначается символом "⊂".

Может случиться, что элементы одного класса будут элементами другого класса, а элементы последнего - элементами первого, т.е. если К 1⊂ К 2и К 2⊂ К 1, тогда К 1= К 2.

Очевидно, что каждый класс может рассматриваться как подкласс самого себя, но в таком случае он представляет мало интереса, и поэтому такой подкласс называют несобственным. В отличие от этого собственным подклассом (частью класса) называют множество элементов, которые одновременно принадлежат обоим классам, причем элементы подкласса составляют лишь часть элементов класса.

Отношения между классами характеризуются следующими основными законами:

1. Для всякого класса К К ⊂ К.

2. Если K 1⊂ К 2, а К 2⊂ К 1, то К 1= К 2.

3. Если К 1⊂ К 2, а К 2⊂ К 3, то К 1⊂ К 3.

4. Если К - не пустой подкласс класса L, и если классы L и М раздельны, то классы А и М также раздельны.

Первый из законов называется законом рефлексивности отношения включения, второй - законом тождества, третий - законом транзитивности, четвертый - характеризует взаимоисключение или раздельность подклассов, что наглядно видно на рис. 12.

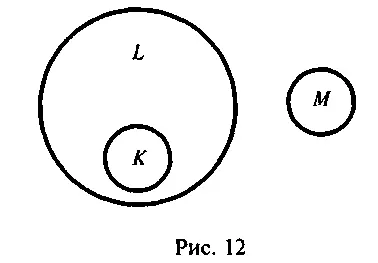
Перечисленные законы вместе с некоторыми другими положениями составляют группу законов категорического силлогизма.

Отсюда можно заключить, что силлогистика, а также традиционная логика, основывающаяся на ней, может быть сведена к теории отношений между классами. Легко убедиться, что два произвольных класса К 1и К 2могут находиться друг к другу в следующих отношениях:

1) классы могут быть тождественными, т.е. К 1= К 2;

2) класс K 1может быть собственным подклассом К 2, т.е. К 1 ⊂К 2;

3) классы K 1и К 2частично совпадают или пересекаются;

4) классы К 1и К 2взаимно исключают друг друга или раздельны.

Такой переход от рассмотрения отношений между свойствами предметов к анализу отношений между классами предметов, обладающих этими свойствами, значительно облегчает исследование и, что особенно существенно, сводит традиционную силлогистику к теории отношений между классами. Отношения же между классами можно свести к исчислению одноместных предикатов. Для иллюстрации рассмотрим силлогизм модуса "Barbara", который в общем виде формулируется так: "Все М есть Р. Все S есть М. Поэтому все S есть Р", а символически записывается следующим образом:

(х) (М(х) → Р(х)), (х) (S(x) → М(х)) | = (х) (S(x) → Р(х)).

Предикаты, которые встречаются здесь, одноместные, выражающие отношение свойства к предмету. Современная же логика имеет дело с многоместными предикатами, характеризующими отношения между различными предметами. Отсюда становится ясным, что силлогистика составляет лишь небольшую часть логики предикатов. Поскольку, однако, силлогизмы формулируются на естественном языке, то они по-прежнему широко используются не только в повседневных, но и научных рассуждениях.

К несиллогистическим дедуктивным рассуждениям, которые изучались в традиционной логике и до сих пор часто используются на практике, относятся некоторые особые формы выводов. Большей частью они представляют собой комбинацию таких посылок, в которых категорические суждения объединяются с условными или с разделительными. Логически необходимый характер заключения в таких рассуждениях обеспечивается тем, что другие возможности вывода исключаются благодаря категорическому суждению.

Обратимся сначала к условно-категорическим умозаключениям, в которых одна посылка является условным суждением, а другая - простым категорическим суждением. Очевидно, что посылки такого рассуждения должны быть логически связанными друг с другом. Эта связь выражается в том, что термины, которые встречаются в категорическом суждении, должны также фигурировать либо в основании, либо в следствии условного суждения.