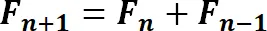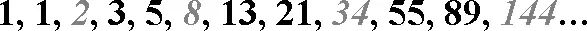Валерий Борискин - Альтернативный волновой анализ

Начнем, пожалуй, с самого простого, с ряда чисел Фибоначчи, тем более что коэффициенты Фибоначчи непосредственно вытекают из данного ряда. Многие знают, что правило, по которому образуются числа Фибоначчи, очень простое: первые два члена – единицы, а затем, каждый последующий член ряда получается путем сложения двух предшествующих значений .

Например, 3 + 5 = 8, 5 + 8 = 13 и т. д.

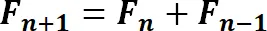
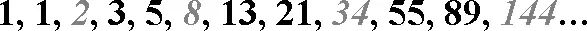
Чем же так интересен ряд чисел Фибоначчи, кроме того, что его значения очень часто используются для записи периодов различных индикаторов? Последовательность Фибоначчи имеет несколько весьма показательных закономерностей, которые, кстати, и определяют коэффициенты Фибоначчи.

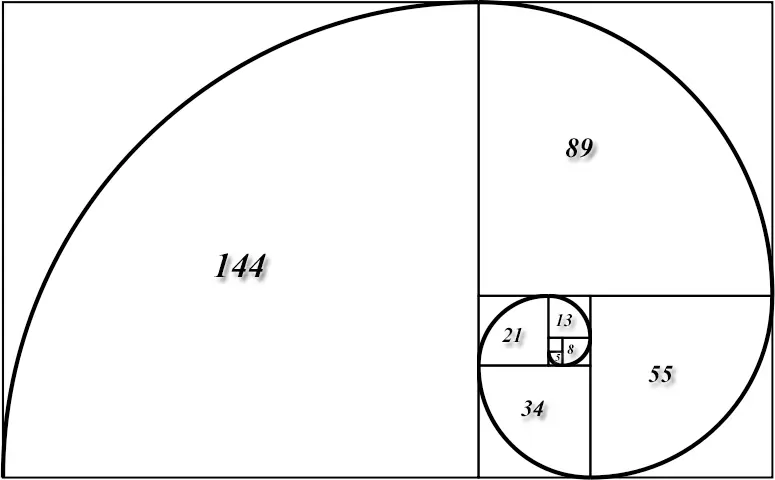
Рисунок 2.1. Числа Фибоначчи и спираль Фибоначчи

1. Сумма двух предыдущих чисел ряда соответствует последующему числу в последовательности. Например: 3 + 5 = 8; 5 + 8 = 13 и т. д. (рис. 2.1).

2. Каждое третье число ряда четное, то есть кратно двум. Например: 2: 2 = 1, 8: 2 = 4, 34: 2 = 17, 144: 2 = 72.

3. Отношение текущего числа ряда к последующему числу (F n/F n+1) стремится к значению 0,618, за исключением первых четырех чисел ряда. При этом значения соотношений колеблются вокруг величины 0,618 то в большую, то в меньшую сторону, и размах колебаний постепенно уменьшается.

4. Отношение текущего числа ряда к предыдущему числу (F n/F n-1) стремится к значению 1,618 ( величина, обратная 0,618 ), за исключением первых четырех чисел ряда. При этом соотношения колеблются вокруг величины 1,618 то в большую, то в меньшую сторону, и размах колебаний постепенно уменьшается и уже после второго значения начинает соответствовать величинам отклонения для 0,618.

5. Отношение текущего числа ряда к последующему числу через одно (Fn/F n+2) стремится к значению 0,382 (в сумме с 0,618 дает 1) , за исключением первых четырех чисел ряда. При этом значения соотношений колеблются вокруг величины 0,382 то в большую, то в меньшую сторону, и размах колебаний постепенно уменьшается и уже после второго значения начинает соответствовать величинам отклонения для 0,618 и 1,618.

6. Отношение текущего числа ряда к предыдущему числу через одно (F n/F n) -2стремится к значению 2,618 (величина, обратная 0,382), за исключением первых четырех чисел ряда. При этом значения соотношений колеблются вокруг величины 2,618 то в большую, то в меньшую сторону, и размах колебаний постепенно уменьшается и уже после второго значения начинает соответствовать величинам отклонения для 0,618, 1,618 и 0,382.

Полученные нами значения называются коэффициентами Фибоначчи и активно используются большинством трейдеров в биржевой торговле с целью определения соотношений длин волн друг относительно друга.

Ранее я уже указывал на тот факт, что согласно волновому анализу, все финансовые рынки стремятся к равновесию, которое объясняется тем, что предложение стремится удовлетворить спрос, и наоборот. В результате это приводит к тому, что цена начинает формировать волны, размеры которых соответствуют пропорциям «золотого сечения». Попробуем разобраться в том, что это такое и каким образом данное правило связано с рассматриваемым нами рядом чисел Фибоначчи.

По одной из легенд считается, что математик Фибоначчи вывел свой ряд, наблюдая за совершенством пропорций великой пирамиды в Гизе. Сегодня известно, что эти пирамиды построены по правилу «золотого сечения», для объяснения которого можно использовать простую формулировку: золотое сечение представляет собой деление непрерывной величины на части в таком соотношении, при котором большая часть относится к меньшей части, точно так же, как вся величина относится к большей части» .

Вообще, «золотое сечение» рассматривается как аналог идеальной пропорции, истинной мерой соотношения частей между собой. Если разделить отрезок на две неравные части, то только в случае «золотого сечения» полученные части будут гармонично соотноситься как друг с другом, так и с целым отрезком в общем.