Феликс Филатов - Клеймо создателя

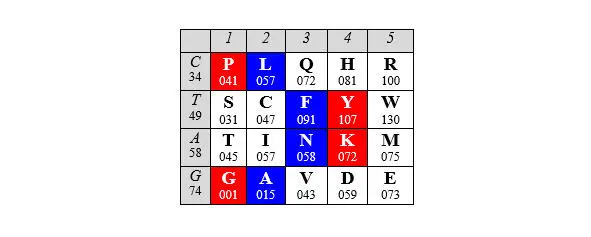
сводит число возможных версий трехмерной модели кода к единственной:

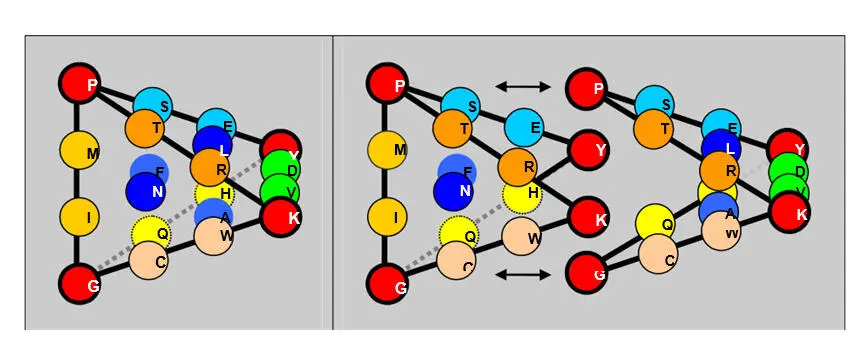
Правда, равновесную по граням модель можно также построить, заменив ребра QHи VDна QVи НDи сохранив, таким образом, симметричный рисунок реберных мономеров в составе матрицы, однако, эта версия потребует сделать формулировку принципа сборки тетраэдра более свободной, поскольку наш тетраэдр характеризуется также полной симметрией по граням аминокислот двух арс-классов:на каждую его грань приходится равное (по 5) число мономеров-аминокислот каждого класса.

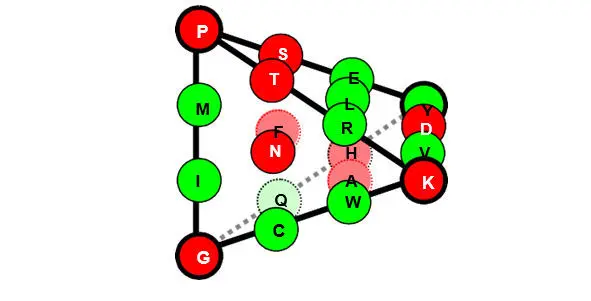
Других столь же простых условий сборки тетраэдра с нуклонным равенством граней не существует. Также (естественно) не удается сформировать подобный тетраэдр, используя значения порядковых номеров этих мономеров в качестве их альтернативных параметров. Количественная симметрия имеет место только в отношении номеров инвариантных мономеров сплошной последовательности аминокислот (независимой от арс-класса): суммы номеров мономеров вершин полученного тетраэдра и центров его граней равны (и в случае нумерации по нарастанию нуклонной массы составляют замечательное – в контексте этой и предыдущей глав – десятичное число 37).

Инвариантные мономеры и сами по себе обладают целой серией собственных симметрий по первым, вторым и третьим основаниям своих кодонов, что является следствием их положения в составе матрицы кода. Читатель может самостоятельно организовать и проанализировать таблицы, необходимые для демонстрации этих симметрий.

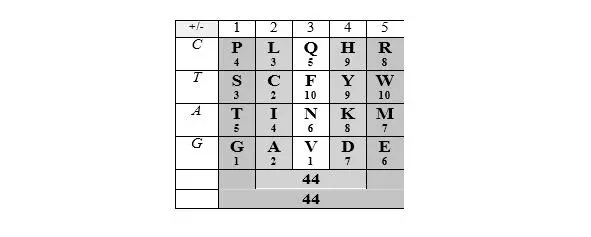
В формате позиционных номеров аминокислот, принадлежащих к тому или другому арс-классу, отметим, что значения колоночных и построчных суммаций матрицы генетического кода имеют весьма замечательный вид: линейное нарастание сумм порядковых номеров центральных колонок, выраженное двух– или трехзначными инфрмационными символами, в комбинации со сдвиговой для трехзначных чисел (или зеркальной для двузначных) симметрией цифр в крайних колонках, а также в строках, соответствующих первым комплементарным основаниям кодонов:

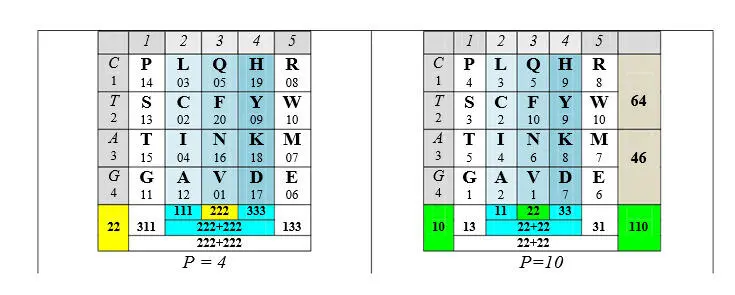
Читателю предлагается обратить внимание на следующее:

цифровые гомодублеты, как носители информации о симметрии, имеют здесь не меньшее значение, чем гомотриплеты;

в тех случаях, когда значения линейно нарастающих сумм порядковых номеров центральных колонок в той или иной системе счисления не подчеркнуто гомодублетами 11—22—33 или гомотриплетами 111—222—333, цифровые симметрии сумм крайних колонок «комплементарны», так что сумма двух крайних колонок представляет собой следующий гомодублет (44) или гомотриплет (444);

в тех случаях, когда значения сумм колонок или строк имеют неодинаковое число разрядов в той или другой системе счисления, цифровые симметрии сумм крайних колонок невыразительны;

то обстоятельство, что таблица справа (где арс-классы представлены как самостоятельные группы, то есть члены каждой имеют собственную, а не последовательную, нумерацию) демонстрирует симметрии не только по колонкам, но и по строкам, свидетельствует об определенной независимости классов;

наконец, то обстоятельство, что обе таблицы демонстрируют не только числовые, но и цифровые симметрии, как будто поддерживает логику сравнения числового значения и цифрового порядка, которые – имея общее выражение – характеризуют описанный в предыдущей главе виртуальный олигопептид.

Паттерн этих матричных симметрий в значениях порядковых номеров аминокислот сходен с паттерном симметрий матрицы в значениях их нуклонных масс (см. выше):

…………………

И хватит, пожалуй. Автору не хочется больше надоедать Читателю похожими друг на друга таблицами и «интересными» числами. Пора подумать, что все они означают. Сумбур и брызги негромкого, но явственно различимого ритма Музыки Сфер ? Сто лет назад Бернард Шоу (одно время музыкальный критик) – словно предчувствуя расцвет сегодняшней глянцевой «звездятины» – заметил, что музыка – это алкоголь осужденных грешников 62. Справедливо, конечно, если скорбеть животом в такт второй симфонии Бетховена (http://galicarnax.livejournal.com/25217.html). Но так ли уж нужны стигматы святой Терезе ? Так ли они ей желанны ?