Феликс Филатов - Клеймо создателя

При метеоритных ударах таких масштабов возникали трещины, из которых выделялась горячая вода, насыщенная органическими молекулами, и такие трещины могли стать очагами предбиологических процессов, которые привели к быстрому появлению жизни по окончании бомбардировки.

Жизнь могла возникнуть именно в горячей воде таких гидротермальных очагов. По мнению Кринга и Коэна, условия в трещинах метеоритов были настолько благоприятными для этого, что первые живые клетки могли появиться там уже через несколько сот тысяч лет после конца бомбардировки, то есть примерно 3,85 миллиардов лет тому назад. Эта дата, действительно, близка к возрасту обнаруженных в последние годы первых признаков жизни на Земле.

…………………

Немного о номере этой главы. Читатель, который уже ожидал, что им станет число 31 , поскольку очевидная привязанность Автора к триплету 111 , как будто, требует перехода от представления этого гомотриплета в четверичной системе ( 21 ) к представлению его в пятеричной, будет приятно разочарован доверием Автора к своей сообразительности. Автор принимает, что Читатель давно усвоил и само понятие о системах счисления, и «равноправие» таких систем с различными основаниями. Другое дело – человеческая культура, где некоторые из этих систем исторически акцентированы (например, десятичная, как удобная для счета пальцами обеих рук, или пятеричная, которую – из тех же соображений – еще в XIX веке использовали китайцы, освободив другую руку для других дел). Гомотриплет (информационная сигнатура с тремя одинаковыми знаками) 111 выделен в таблице ниже, в которой – как и в предыдущем случае ( Глава 21 ), но уже для пятеричной системы – он соответствует децимальному числу 31 . Первые тридцать пять десятичных чисел (темные колонки) в пятеричной системе счисления записываются так (светлые колонки):

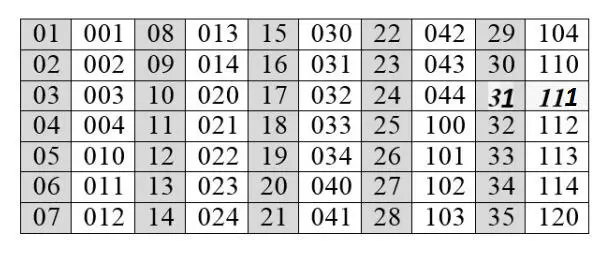
В соответствии с определением, пятеричная система счисления использует пять символов-цифр: 1, 2, 3, 4 и 0.

Вместо того, чтобы утомлять читателя однотипным комментарием, посвящая его номеру очередной главы, который соответствует одному и тому же числу в очередной системе счисления, Автору кажется гораздо выигрышней сразу представить это число общей таблицей в серии систем с основаниями от 1 до 20 (крупный шрифт – десятичные числа N, соответствующие числу 111 в системах счисления, основания которых, P , обозначены мелким шрифтом):

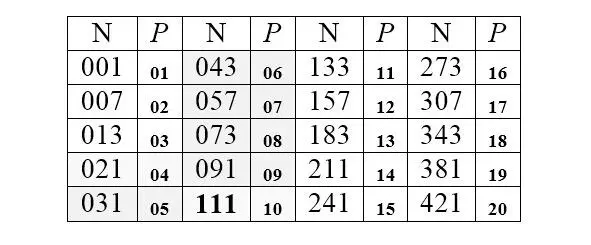
Таблица, естественно, открывается числом 1. Система счисления с основанием 1 системой в принятом смысле, вообще говоря, не является. Число 1111 в такой «системе» графически означает всего лишь десятичную тройку ( 3= 1+ 1+ 1), соответствующую тройке римской – III(числу без разрядов). Таким же образом десятичному 111 соответствуют сто одиннадцать символов 1 , представленных также без всяких разрядов, поскольку символа ноля в « сингулярной » (унарной) системе нет. Вот как оно выглядит (для удобства восприятия это число изображено тремя равными строками по 37 единиц):

1111111111111111111111111111111111111

1111111111111111111111111111111111111

1111111111111111111111111111111111111

Обратив, таким образом, внимание на число 1 и вспомнив о прошлом человечества, когда сингулярная система счисления была и единственной, и единственно возможной, Автор и главу эту хотел было обозначить приведенным трехстрочным числом. Но ни три римские цифры, ни три строки цифр арабских не показались ему уместными или «соответствующими» в контексте рассказа, и он ограничился «одноразрядным» числом, графемой (или нумералом ) 1 . Да и навязчивым быть не хотелось со своими предпочтениями – до поры, до времени.

Мы уже упоминали об особенности четверичного числа 111 4 (21) – способности делиться без остатка на три. Такой же способностью обладает семеричное число 111 7 ( 57 ) и десятичное 111 (системы с Р > 10 мы здесь не рассматриваем). Наибольшие общие делители d каждого из этих чисел равны: 7 = 13 4, 19 = 25 7 и 37 = 37 10 . Делимость трехзначного числа в этих системах на d следует прямой (слева направо) пермутации: если на 37 (в системе P =10) делится, например, число 925, то тем же свойством обладают также числа 259 и 592 (но не 529 и не 295). Из этого следует делимость на 37 всех гомотриплетов – 111 , 222 , 333 и т. д. Те же рассуждения справедливы и в отношении чисел четверичной и семеричной систем. Владимир Щербак упоминает Луку Пачиоли, известного математика Возрождения, «изобретателя» бухгалтерского учета, друга и учителя математики самого Леонардо, которого « изумила цифровая симметрия десятичных чисел, кратных 37 … Если одна из целей такой симметрии – привлечь внимание исследователя, то реакция Пачиоли говорит, что эта цель достижима ». Привлечет ли такое же ИХ внимание позолоченная пластинка «Вояджера»?