Вопросы для самопроверки:
– Будет ли общая численность математиков расти, а не уменьшаться при таких условиях?
– Предположим, вы не знаете эффективной «плодовитости», но знаете, что численность 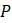 стабильна (неизменна) с течением времени. Какой должна быть
стабильна (неизменна) с течением времени. Какой должна быть 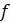 ? (Подсказка: поймите, что такое
? (Подсказка: поймите, что такое 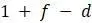 , если численность стабильна?) Если каждый год выпускается 200 молодых специалистов, какая их часть должна оставаться в системе и обучать математиков следующего поколения?
, если численность стабильна?) Если каждый год выпускается 200 молодых специалистов, какая их часть должна оставаться в системе и обучать математиков следующего поколения?
Обратите внимание, что в этой последней модели мы игнорировали тех математиков, кто не участвует в обучении математиков следующего поколения. Это на самом деле довольно распространенный подход и упрощает модель. Однако это означает, что делаются дополнительные предположения. Для конкретного направления точное количество учителей может мало влиять на то, как растет численность специалистов. Возможно, учителя всегда встречаются примерно в равном количестве с узкими специалистами, так что мы знаем, что общая численность людей, посвятивших жизнь математике, просто вдвое превышает число учителей математики. С другой стороны, численность профессиональных математиков может вести себя иначе, чем численность учителей математики, но независимо от того, мало ли учителей или их много, всегда достаточно, чтобы появление учителей происходило непрестанно. Таким образом, именно численность учителей математики является важным параметром для отслеживания, чтобы понять долгосрочный рост или сокращение числа профессиональных математиков в стране.
Вопросы для самопроверки:
– Можете ли вы представить себе обстоятельства, при которых игнорирование уменьшения числа профессионалов той или оной области было бы хорошей идеей?
Так что же такое разностное уравнение? Теперь, когда увидели разностное уравнение на примере, можно попытаться дать строгое определение: разностное уравнение – это формула, выражающая значения некоторой величины 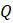 в терминах предыдущих значений
в терминах предыдущих значений 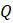 . Таким образом, если
. Таким образом, если 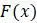 является какой-либо функцией, то
является какой-либо функцией, то 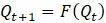 называется разностным уравнением. В предыдущем примере использовалась
называется разностным уравнением. В предыдущем примере использовалась 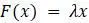 , но часто
, но часто 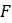 будет более сложным.
будет более сложным.
Изучая разностные уравнения и их приложения, рассмотрим два основных вопроса: 1) Как найти подходящее разностное уравнение для моделирования ситуации? 2) Как понять поведение модели разностных уравнений после того, как её нашли?
Обе эти задачи бывают довольно трудны. Тем не менее, обязательно научитесь моделировать с помощью разностных уравнений, глядя на математические модели, используемые разными авторами в классической литературе, а затем создадите собственные модели. Однако, честно говоря, это не обязательно исключит столкновение с принципиально неразрешимой проблемой. Что касается понимания поведения, которое моделируется разностным уравнением, то обычно не представляется возможным найти явную формулу, как было сделано выше для 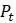 , описывающего численность популяции в мальтузианской модели. Вместо этого разрабатываются методы извлечения менее точной, но качественной, а не количественной информации из модели.
, описывающего численность популяции в мальтузианской модели. Вместо этого разрабатываются методы извлечения менее точной, но качественной, а не количественной информации из модели.
Конкретное разностное уравнение, обсуждаемое в этом разделе, иногда называют экспоненциальной или геометрической моделью, поскольку модель приводит к экспоненциальному росту и ассоциируется с именем Томаса Мальтуса. Математики, однако, склонны сосредотачиваться на форме уравнения 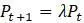 и говорить, что модель линейна. Такая терминология может сбивать с толку, но она важна, когда линейная модель описывает экспоненциальный рост или убывание.
и говорить, что модель линейна. Такая терминология может сбивать с толку, но она важна, когда линейная модель описывает экспоненциальный рост или убывание.
Читать дальше

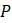 стабильна (неизменна) с течением времени. Какой должна быть
стабильна (неизменна) с течением времени. Какой должна быть 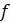 ? (Подсказка: поймите, что такое
? (Подсказка: поймите, что такое 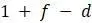 , если численность стабильна?) Если каждый год выпускается 200 молодых специалистов, какая их часть должна оставаться в системе и обучать математиков следующего поколения?
, если численность стабильна?) Если каждый год выпускается 200 молодых специалистов, какая их часть должна оставаться в системе и обучать математиков следующего поколения?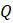 в терминах предыдущих значений
в терминах предыдущих значений 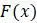 является какой-либо функцией, то
является какой-либо функцией, то 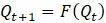 называется разностным уравнением. В предыдущем примере использовалась
называется разностным уравнением. В предыдущем примере использовалась 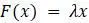 , но часто
, но часто 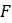 будет более сложным.
будет более сложным.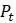 , описывающего численность популяции в мальтузианской модели. Вместо этого разрабатываются методы извлечения менее точной, но качественной, а не количественной информации из модели.
, описывающего численность популяции в мальтузианской модели. Вместо этого разрабатываются методы извлечения менее точной, но качественной, а не количественной информации из модели.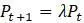 и говорить, что модель линейна. Такая терминология может сбивать с толку, но она важна, когда линейная модель описывает экспоненциальный рост или убывание.
и говорить, что модель линейна. Такая терминология может сбивать с толку, но она важна, когда линейная модель описывает экспоненциальный рост или убывание.










