Денис Соломатин - Математические модели в естественнонаучном образовании. Том I
Здесь есть возможность читать онлайн «Денис Соломатин - Математические модели в естественнонаучном образовании. Том I» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Год выпуска: 2022, Жанр: Биология, Медицина, Математика, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Математические модели в естественнонаучном образовании. Том I
- Автор:
- Жанр:
- Год:2022
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 2
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Математические модели в естественнонаучном образовании. Том I: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Математические модели в естественнонаучном образовании. Том I»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.

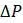 зависит от
зависит от 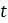 , поэтому можно встретить подстрочный индекс
, поэтому можно встретить подстрочный индекс 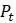 , а не только приращения
, а не только приращения 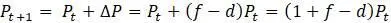 . Объединив константы вместе, обозначив за
. Объединив константы вместе, обозначив за 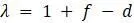 , модель стала гораздо проще:
, модель стала гораздо проще: 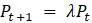 .
.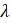 конечной скоростью роста населения. (Слово «конечный» используется, чтобы отличить это число от любого вида мгновенной скорости, которая включала бы производную, как вы знаете из курса дифференциального исчисления. Для значений
конечной скоростью роста населения. (Слово «конечный» используется, чтобы отличить это число от любого вида мгновенной скорости, которая включала бы производную, как вы знаете из курса дифференциального исчисления. Для значений 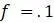 ,
, 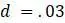 , и
, и 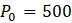 использованных ранее, вся модель теперь имеет вид
использованных ранее, вся модель теперь имеет вид 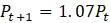 , где
, где 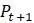 через
через 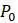 , является его начальным условием. С этими двумя уравнениями легко составить таблицу значений численности
, является его начальным условием. С этими двумя уравнениями легко составить таблицу значений численности 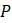 с течением времени, как в таблице 1.1.
с течением времени, как в таблице 1.1.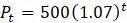 . На этой модели теперь легко предсказать численность популяции в любое время.
. На этой модели теперь легко предсказать численность популяции в любое время.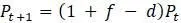 разностным уравнением, когда разность
разностным уравнением, когда разность 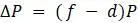 эквивалентны, поэтому любое из них разумно определять одним и тем же термином.
эквивалентны, поэтому любое из них разумно определять одним и тем же термином.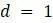 , в то время как эффективная «плодовитость» системы равна
, в то время как эффективная «плодовитость» системы равна 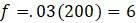 . Следовательно,
. Следовательно, 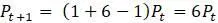 .
.










