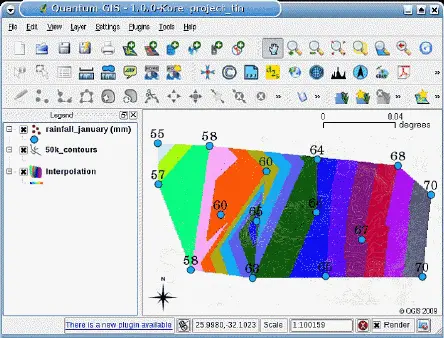
Рисунок 91: Триангуляция Делоне на основе нерегулярных точек сбора данных об осадках.
О чем стоит помнить
Важно помнить, что не существует такого метода интерполяции, который подходил бы ко всем ситуациям. Некоторые обеспечивают более точный результат, но требовательны к вычислительным ресурсам компьютера и исполняются дольше. У всех есть достоинства и недостатки. Выбор определенного метода интерполяции зависит от особенностей входных данных, требуемого типа итоговой поверхности и уровня допустимых ошибок оценки величин. В целом, рекомендуется производить три этапа оценки:
1. Оценить входные данные с точки зрения пространственного распределения точек и подумать о том, какой характер носит распределение моделируемой величины (плавный, сконцентрированный вокруг точек и др.). Это поможет определить подходящий метод интерполяции.
2. Рассмотреть задачу и найти метод, который подходит наилучшим образом. Если есть сомнения, можно попробовать несколько методов.
3. Сравнить результаты и выбрать лучший результат, а следовательно — самый подходящий метод.
Поначалу этот процесс будет выглядеть сложным, но по мере приобретения опыта работы с разными методами интерполяции время, необходимое для генерации подходящей поверхности, сильно сократится.
Другие методы интерполяции
Хотя в данном разделе мы остановились на методах IDWи TIN, существует множество других методов интерполяции, например RST(англ. Regularized Splines with Tension, рус. Регуляризированный Сплайн с Натяжением), Кригинг (англ. Kriging) или трендовая интерполяция (англ. Trend Surface Interpolation). Дополнительная информация о них приведена по ссылке ниже.
Что мы узнали?
Закрепим изученный материал:
• Интерполяцияиспользует векторные точки с известными значениями той или иной величины для оценки этой величины в неизвестных точках и создает растровую поверхность, покрывающую всю область исследования.
•Результат интерполяции — растровый слойтого или иного формата.
•Для оптимальной оценки величины важно выбрать подходящий метод интерполяции.
• IDW-интерполяцияприсваивает входным точкам коэффициенты взвешивания так, что воздействие точек затухает с увеличением расстояния до новой точки, где производится оценка значения величины.
• TIN-интерполяцияиспользует входные точки для создания поверхности, состоящей из прилегающих друг к другу треугольников, основываясь на пространственном распределении этих точек.
Попробуйте сами!
Ниже приведено несколько примеров практических заданий для Ваших учеников:
•Департамент Сельского Хозяйства планирует перевод земель в с/х использование, но помимо типа почв для этого нужно знать, достаточно ли осадков выпадает в данной области. Вся информация, которой они располагают, — это данные с нескольких метеостанций. Создайте поверхность интерполяции, которая показывает участки с наибольшим количеством осадков на территории.
•Департамент туризма хочет опубликовать информацию о погодных условиях в январе и феврале. У них есть данные метеостанций о температуре, осадках и силе ветра, и они попросили Вас найти территории с оптимальными условиями для туристов, а именно — мягкими температурами, отсутствием осадков и слабыми ветрами. Можете ли Вы найти эти территории, используя инструменты ГИС?
Если у Вас нет компьютера
Вы можете использовать лист топографической карты и линейку для оценки высот между горизонталями или температуры между гипотетическими метеостанциями. Например, если температура на станции А равна 20 °C, а температура на станции В равна 24 °C, то в точке, лежащей ровно посередине между этими станциями, температура примет значение в 22 °C.
Дополнительные материалы
Книги:
•Chang, Kang-Tsung (2006): Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. (ISBN 0070658986)
•DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. (ISBN 9814126195)
•Mitas, L., Mitasova, H. (1999): Spatial Interpolation. In: P.Longley, M.F. Goodchild, D.J. Maguire, D.W.Rhind (Eds.), Geographical Information Systems: Principles, Techniques, Management and Applications, Wiley.
Веб-сайты:
http://en.wikipedia.org/wiki/Interpolation
http://en.wikipedia.org/wiki/Delaunay_triangulation
http://www.agt.bme.hu/public_e/funcint/funcint.html
Читать дальше













