Олег Мединов - Excel. Мультимедийный курс

1. В ячейку R1C3введите текст Длина окружности.

2. Щелкните кнопкой мыши на ячейке R2C3.

3. Введите знак =.

4. Введите цифру 2.

5. Введите знак умножения (*).

6. Введите число π (3,14).

7. Введите знак умножения (*).

8. Щелкните кнопкой мыши на ячейке R2C1. В формуле появится относительный адрес первой ячейки, в которой мы указываем радиус. У вас должна получиться формула следующего вида: =2*3,14*RC[-2].

9. Нажмите клавишу Enter. Если в ячейке R2C1указано какое-либо число, вы немедленно получите результат вычисления длины окружности в ячейке R2C3.

10. Введите новое значение радиуса в ячейку R2C1и нажмите клавишу Enter. Обратите внимание, что в ячейках R2C2и R2C3значения изменились одновременно. Сколько бы вы ни создали формул, использующих значение ячейки R2C1, результат их вычисления будет обновляться при изменении значения в этой ячейке (рис. 6.2).

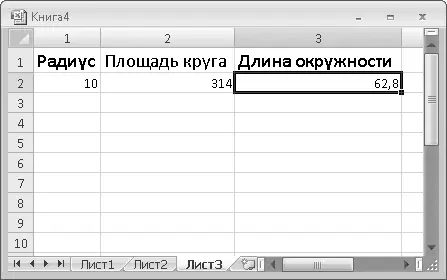
Рис. 6.2.Формулы в ячейках R2C2 и R2C3 используют значение ячейки R2C1

Приведу арифметические операторы, которые вы можете использовать при создании формул:

+– оператор сложения;

–– оператор вычитания;

*– оператор умножения;

/– оператор деления;

^– оператор возведения в степень. Этот оператор ставится после числа (или переменной), которое возводится в степень. После этого оператора указывается значение степени, которое может быть как числом, так и переменной (переменной в данном случае мы считаем ссылку на ячейку со значением);

%– оператор вычисления процента.

Вы заметили, что при создании формул мы указывали ячейку R2C1, но в формулах появлялись значения RC[-1]и RC[-2]? Ранее упоминалось, что ячейка может иметь абсолютный и относительный адреса. Относительный адрес указывает путь к ячейке относительно ячейки с формулой. Так, в формуле вычисления площади круга значение RC[-1]показывает, что данные нужно взять из ячейки той же строки, но на один столбец левее. В формуле длины окружности значение RC[-2]сообщает, что данные необходимо взять из ячейки той же строки, но на два столбца левее. Конечно, вы можете в формулах указать и абсолютный адрес ячейки.

Что дает относительный адрес в формуле? Чтобы получить ответ, выполните следующие действия.

1. Выделите ячейку R2C2, то есть ячейку с формулой площади круга.

2. Установите указатель мыши на рамку выделения, чтобы он принял вид четырех противоположно направленных стрелок.

3. Нажав и удерживая кнопку мыши, перетащите рамку выделения в ячейку R6C3и отпустите кнопку мыши. Результат вычисления площади круга появится в ячейке R6C3.

4. Попробуйте изменить значения радиуса круга в ячейке R2C2. В ячейке R6C3обновится значение площади.

5. Выделите ячейку R6C3и посмотрите на строку формул. Формула несколько изменилась, и теперь она выглядит так: =3,14*R[-4]C[-2]^2. Выражение R[-4]C[-2]означает, что данные (радиус) следует искать в ячейке, расположенной на четыре строки выше и два столбца левее.

Куда бы вы ни перетаскивали ячейку с формулой, относительный адрес ячейки радиуса будет меняться и указывать именно на ячейку R2C1. Точно такой же результат вы получите, изменив положение ячейки R2C1(ячейки со значением радиуса). Куда бы вы ни переместили эту ячейку, формулы по-прежнему будут возвращать верный результат вычислений, но относительный адрес ячейки со значением радиуса в них будет меняться. Относительный адрес в формуле как бы «цепляется» к ячейке, на которую он ссылается, и не позволяет разорвать эту связь при любом перемещении ячейки формулы или ячеек данных.

Приведу пример, который наглядно покажет преимущества относительного адреса перед абсолютным. Мы создадим таблицу вычислений площади круга в зависимости от радиуса, чтобы увидеть несколько значений площади при разных радиусах.

1. Верните данные с радиусом и формулой на свои места (соответственно в ячейки R2C1и R2C2).

2. Выделите ячейку R2C2.

3. Скопируйте ее содержимое в буфер обмена. Для этого нажмите кнопку Копироватьна вкладке Главнаяили сочетание клавиш Ctrl+Insert.