Татьяна Соколова - AutoCAD 2009 для студента. Самоучитель

При работе в трехмерном пространстве в AutoCAD все системы координат формируются по правилу правой руки . Оно определяет положительное направление оси Z трехмерной системы координат при известных направлениях осей X и Y , а также положительное направление вращения вокруг любой из осей трехмерных координат.

Для определения положительных направлений осей необходимо поднести тыльную сторону кисти правой руки к экрану монитора и направить большой палец параллельно оси X , а указательный – по оси Y . Если согнуть средний палец перпендикулярно ладони, как показано на рис. 4.2 справа, то он будет указывать положительное направление оси Z .

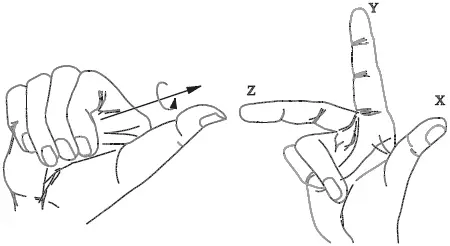
Рис. 4.2.Правило правой руки

Для определения положительного направления вращения следует ориентировать большой палец правой руки в положительном направлении оси и согнуть остальные пальцы, как показано на рис. 4.2 слева. Положительное направление вращения совпадает с направлением, указываемым согнутыми пальцами.

Трехмерные декартовы координаты ( x , y , z ) вводятся аналогично двумерным ( x , y ). Дополнительно к координатам по осям X и Y необходимо ввести еще и значение по оси Z . На самом деле в AutoCAD не существует двумерных координат, и если введены значения только x и y , это означает, что отсутствующая координата z берется по умолчанию равной нулю. При указании декартовых трехмерных координат с клавиатуры вводятся три числа через запятую, например:

3,5,2

В трехмерном пространстве, так же как и в двумерном, широко используются и абсолютные координаты (отсчитываемые от начала координат), и относительные (отсчитываемые от последней указанной точки). Признак относительных координат – символ @ перед координатами вводимой точки, которая в этом случае берется относительно последней введенной точки.

Как было сказано выше, в AutoCAD существуют: мировая система координат World Coordinate System, WCS, и пользовательская система координат User Coordinate System, UCS. Ось X мировой системы координат направлена горизонтально, ось Y – вертикально, а ось Z проходит перпендикулярно плоскости XY . Начало координат – это точка пересечения осей X и Y , по умолчанию она совмещается с левым нижним углом рисунка. В любой текущий момент активна только одна система координат, которую принято называть текущей . В ней координаты определяются любым доступным способом.

Основное отличие мировой системы координат от пользовательской заключается в том, что мировая система координат может быть только одна (для каждого пространства модели и листа) и она неподвижна. Применение пользовательской системы координат не имеет практически никаких ограничений. Она может быть расположена в любой точке пространства под любым углом к мировой системе координат. Разрешается определять, сохранять и восстанавливать неограниченное количество ПСК. Проще выровнять систему координат с существующим геометрическим объектом, чем определять точное размещение трехмерной точки. ПСК обычно используется для работы с несмежными фрагментами рисунка. Поворот ПСК упрощает указание точек на трехмерных или повернутых видах. Узловые точки и базовые направления, определяемые режимами шаговой привязки SNAP, сетки GRID и ортогонального режима ORTHO, поворачиваются вместе с ПСК.

При работе в ПСК допускается поворачивать ее плоскость XY и смещать начало координат. Все они при вводе отсчитываются относительно текущей пользовательской системы координат. Соответствующая пиктограмма дает возможность судить о положении и ориентации текущей ПСК, помогая визуализировать эту ориентацию относительно мировой системы координат, а также относительно объектов, содержащихся в рисунке.

Пиктограмма ПСК всегда изображается в плоскости XY текущей ПСК и указывает положительное направление осей X и Y . Сама пиктограмма может располагаться как в начале пользовательской системы координат, так и в другом месте. Эту позицию регулирует команда управления пиктограммой системы координат UCSICON. С помощью той же команды можно выбрать одну из пиктограмм, размер, цвет, тип стрелок осей и толщины линий которых можно изменить (рис. 4.3).