Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> type(123,integer);

> type(123.,integer);

> type(123/456,rational);

> type(1./3,rational);

> type(1/2,fraction);

> type(0.5,fraction);

В Maple возможна работа с числами, имеющими различное основание (base), в частности, с двоичными числами (основание 2 — binary), восьмеричными (основание 8 — octal) и шестнадцатиричными (основание 16 — hex). Функция convert позволяет легко преобразовывать форматы чисел:

> convert(12345,binary);

> convert(%,decimal,binary);

> convert(12345,octal);

> convert(123456,hex);

> convert(%,decimal,hex);

Помимо приведенных вариантов функция convert имеет еще ряд других форм. С ними можно познакомиться с помощью справки по этой мощной функции. В дальнейшем будет приведен ряд других применений этой функции.

В целом ряде случаев работа вычислителей Maple по умолчанию в области комплексных значений данных нежелательна, поскольку приводит к представлению результатов также в комплексном виде:

> restart:simplify(sqrt(х^2)); ln(-2); solve(х^3-8=0,x);

В связи с этим в Maple введен новый математический пакет расширения RealDomain, переводящий вычисления в область реальных значений данных. Вызов пакета обеспечивается следующим образом:

> restart:with(RealDomain);

Нетрудно заметить, что этот пакет переопределяет элементарные функции и некоторые другие вычислительные функции таким образом, что вычисления с ними ведутся только с реальными (вещественными, действительными) числами. Это видно из представленных ниже примеров:

> simplify(sqrt(х^2));

> ln(-2);

> solve(х^3-8=0,х);

Следует отметить, что вычисляемые выражения при работе с данным пакетом надо размещать после его загрузки.

В старых версиях Maple функция plot нередко отказывалась строить графики функций, значения которых были комплексными числами. Но уже в Maple 8 алгоритм построения графиков переработан. Теперь, если выражение, по которому строится график, в ходе оценивания дает мнимую часть, она отбрасывается, так что строится график только действительной части выражения. Малые по модулю мнимые части также нередко отбрасываются — впрочем, когда именно не совсем ясно.

Рис. 2.4 дает примеры этого. В верхней части документа строятся графики функции квадратного корня от х, логарифма и синуса. Нетрудно заметить, что для квадратного корня и логарифма строится и впрямь только та часть графиков, где значения функций действительны — при х положительном. Для х< 0 строится только график функции синуса, поскольку синус дает вещественные значения при любом x — как положительном, так и отрицательном.

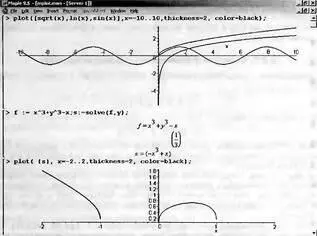
Рис. 2.4. Особые случаи применения функции plot

Еще более интересен случай, представленный снизу рис. 2.4. Здесь функция задана как решение выражения f, которое дает корни в виде комплексных выражений. Несмотря на это возможные части графика функции f(x) строятся.

Сложными являются такие типы данных, которые являются представлением множественных и подчас разнохарактерных объектов. Нередко такие данные включают как часть себя рассмотренные выше простые типы данных.

В системе Maple любые выражения могут включаться в наборы , относящиеся к множественным данным. Такие наборы в виде множеств создаются с помощью фигурных скобок { }:

> {a,b,a,a,b,d,e,c,d};

> {10,2+3,4+4,8,5,1};

> {`Hello` ,`my`,`friend`};

Отличительная черта множеств — автоматическое устранение из них повторяющихся по значению элементов. Кроме того, Maple расставляет элементы множеств в определенном порядке — числа в порядке увеличения значения, а символы и строки в алфавитном порядке. Для множеств нет строгого математического определения, и мы будем считать их наборами, удовлетворяющими перечисленным выше признакам.