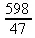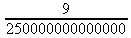Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Некоторые операторы представлены двумя символами — например, оператор присваивания переменным их значения := содержит двоеточие и знак равенства. В таких операторах между символами недопустим знак пробела. Однако его можно использовать между отдельными частями выражений — так, (a+b)/c эквивалентно (a + b) / c.

Maple обеспечивает вполне естественную работу с целыми числами. В частности обеспечивается смена знака числа и выполнение основных арифметических операций с числами. Ввиду общеизвестности арифметических операций их определения не приводятся. Ограничимся примерами простых операций с числами, приведенными ниже:

> 12+34/47;

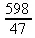
> -12+34*47;

> 12*10^(-15)*3;

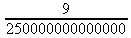
Результаты операций с целыми числами в общем случае представляются рациональными числами , являющимися отношениями целых чисел.

Десятичная точка в числах имеет особый статус — указание ее в любом месте числа, в том числе в конце, делает число вещественным и ведет к переводу вычислений в режим работы с вещественными числами. Например:

> 12.*10^(-15)*3;

Количеством выводимых после десятичной точки цифр можно управлять, задавая значение системной переменной окружения Digits:

> Digits:=3: 1./3;

> Digits:=10; ехр(1.);

> Digits:=40: evalf(Pi);

Как видно из этих примеров, ввод и вывод чисел имеет следующие особенности:

• для отделения целой части мантиссы от дробной используется разделительная точка;

• нулевая мантисса не отображается (число начинается с разделительной точки);

• мантисса отделятся от порядка пробелом, который рассматривается как знак умножения;

• мнимая часть комплексных чисел задается умножением ее на символ мнимой единицы I (квадратный корень из -1);

• по возможности Maple представляет численный результат в виде точного рационального числа (отношения двух целых чисел).

Для работы с числами Maple имеет множество функций. Они будут рассмотрены в дальнейшем. С помощью многофункциональной функции convert Maple может преобразовывать числа с различным основанием (от 2 до 36, в том числе бинарные и шестнадцатиричные) в десятичные числа:

> convert("11001111", decimal, binary);

> convert("1AF.С", decimal, hex);

> convert("Maple", decimal, 36);

Благодаря возможности выполнения символьных вычислений Maple, как и другие СКА, реализует точную арифметику. Это значит, что результат может быть получен с любым числом точных цифр. Однако надо помнить, что идеально точные численные вычисления выполняются только в случае целочисленных операций, например, таких как приведены ниже:

> 101!;

> (101!+1)-101!;

> (10005!)/10000!;

> 2^101-2^100;

> 2^(2^(2^2));

> 2^101-2^100.0;

> Digits;

Обратите внимание на то, что в последнем примере точность резко потеряна, так как показатель степени 100.0 был задан как число с плавающей точкой. Соответственно и результат оказался в форме такого числа. Число верных цифр результата задает системная переменная Digits (по умолчанию 10).

Приведем еще пару примеров точных вычислений некоторых функций (с точностью до 150 знаков мантиссы):

> evalf(ехр(1),150);

> evalf(sin(1.),150);

Разработчики систем Maple и Mathematica утверждают, что в принципе возможны вычисления и с плавающей точкой с заданием до миллиона точных цифр мантиссы. Практически такая точность почти никогда не нужна, по крайней мере для физиков и инженеров. Например, всего 39 точных цифр числа π достаточно, чтобы вычислить длину окружности всей Вселенной с точностью до диаметра атома водорода. Однако истинные математики одно время были просто «помешаны» на вычислении числа π с большой точностью. Кое кто потратил на это всю жизнь. Выдающийся вклад в такие расчеты внес Рамануджан, который еще в 1916 году предложил алгоритмы и формулы для вычисления числа π с произвольной точностью.