Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Имена функций (без указания списка параметров в круглых скобках) тоже по существу являются функциональными операторами. Так что они также могут использоваться при построении графиков упрощенными способами.

В ряде случаев для задания функциональных зависимостей используются заданные параметрически уравнения, например x=f 1 (t) и y=f 2 (t) при изменении переменной t в некоторых пределах. Точки (x, y) наносятся на график в декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме:

plot([f1(t), f2(t), t=tmin..tmax], h, v, p)

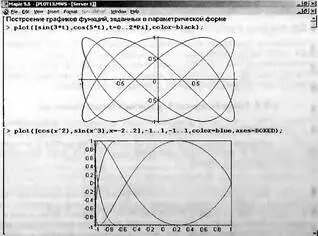
Рис. 8.8. Построение функций, заданных параметрически

Если функции f 1(t) и f 2(t) содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t обычно задается равным 0..2*Pi или -Pi..Pi. К примеру, если задать в качестве функций f 1(t) и f 2(t) функции sin(t) и cos(t), то будет получен график окружности. Рис. 8.8 показывает другие, чуть менее тривиальные примеры построения графиков такого рода.

Задание диапазонов для изменений h и v, а также параметров p не обязательно. Но, как и ранее, они позволяют получить вид графика, удовлетворяющий всем требованиям пользователя.

Графики в полярной системе координат представляют собой линии, которые описывает конец радиус-вектора r(t) при изменении угла t в определенных пределах — от t minдо t max. Построение таких графиков также производится функцией plot, которая для этого записывается в следующем виде:

plot([r(t), theta(t), t=tmin..tmax], h, v, p, coords=polar)

Здесь существенным моментом является задание полярной системы координат параметр coords=polar. Рис. 8.9 дает примеры построения графиков функций в полярной системе координат.

Рис. 8.9. Построение графиков функций в полярной системе координат

Графики параметрических функций и функций в полярной системе координат отличаются огромным разнообразием. Снежинки и узоры мороза на стеклах, некоторые виды кристаллов и многие иные физические объекты подчиняются математическим закономерностям, положенным в основу построения таких графиков.

Трехмерными графиками называют графики, отображающие функции двух переменных z(x, y) . Каждая точка z, таких графиков является высотой (аппликатой) точки, лежащей в плоскости XY и представленной координатами (х i , у i ). Поскольку экран монитора компьютера в первом приближении является плоским, то на деле трехмерные графики представляют собой специальные проекции объемных объектов.

Для построения графиков трехмерных поверхностей Maple имеет встроенную в ядро функцию plot3d. Она может использоваться в следующих форматах:

plot3d(expr1, x=a..b, y=c..d,p)

plot3d(f, a..b, c..d,p)

plot3d([exprf,exprg,exprh], s=a..b, t=c..d,p)

plot3d([f,g,h], a..b, c..d,p)

В двух первых формах plot3d применяется для построения обычного графика одной поверхности, в других формах — для построения графика с параметрической формой задания поверхности. В приведенных формах записи f, g и h — функции; expr1 — выражение, отражающее зависимость от х и у; exprf, exprg и exprh — выражения, задающие поверхность параметрически; s, t, а и b — числовые константы действительного типа; c и d — числовые константы или выражения действительного типа; х, у, s и t — имена независимых переменных; р — управляющие параметры.

С помощью параметров р можно в широких пределах управлять видом трехмерных графиков, выводя или убирая линии каркасной сетки, вводя функциональную окраску поверхностей, меняя угол их обзора и параметры освещения, изменяя вид координатных осей и т.д. Следующие параметры функции plot3d задаются аналогично их заданию для функции plot:

axesfont font color coords font labelfcnt linestyle

numpoints scaling style symbol thickness title titlefont