Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

• PolynomialSolution — решение в форме полинома;

• RationalSolution — решение в форме рационального выражения;

• SeriesSolution — решение в виде ряда;

• UniversalDenominator — решение с универсальным знаменателем (и числителем, равным 1).

Система функциональных уравнений задается либо в виде полной системы sys со списком переменных vars, либо в матричном виде с заданием матрицы коэффициентов системы А и вектора свободных членов b (может отсутствовать) с указанием независимой переменной x и параметра case, имеющего значения 'differential', 'difference' или 'qdifference'. Параметр method, задающий метод EG-исклю-чения может иметь значения 'quasimodular' или 'ordinary'.

Несколько вспомогательных функций пакета LinearFunctionalSystems представлено ниже:

• MatrixTriangularization(mat, m, n, х, It) — триангуляция матрицы mat размера m×n с указанием типа It ('lead' или 'trail');

• CanonicalSystem(shift, sys, vars) или CanonicalSystem(shift, A[, b], x, case) — возвращает систему в каноническом виде (параметр shift задается как 'difference' или 'q-difference', назначение других параметров соответствует указанным выше для других функций);

• ExtendSeries(sol, deg) — расширяет ряд решения sol до расширенного ряда степени deg;

• HomogeneousSystem(homo, sys, vars) или HomogeneousSystem(homo, A[, b], x, case) — преобразует исходную систему в гомогенную с именем homo.

• Properties(sys, vars) или Properties(A[, b], x, case) — возвращает основные свойства системы.

Ряд примеров применения пакета LinearFunctionalSystems представлен в файле lfs и в справке по данному пакету.

Возможности Maple 10 в решении дифференциальных уравнений существенно расширены. Это прежде всего касается решения ряда таких уравнений в аналитическом виде. В частности введен ряд новых опций для функции dsolve, представляющих решения дифференциальных уравнений, например Абеля, Риккати и др. На рис. 7.38 представлен пример решения линейного дифференциального уравнения, представленного через новую специальную функцию Хеуна (Heun). Этот пример описан в самоучителе Maple 10.

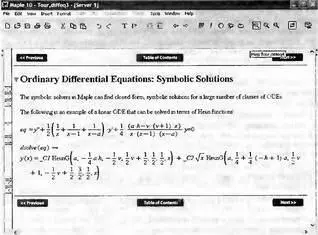
Рис. 7.38. Пример решения линейного дифференциального уравнения

Решатель дифференциальных уравнений Maple 10 способен находить аналитические решения и для большого числа дифференциальных уравнений в частных производных. Пример такого решения из самоучителя Maple 10 представлен на рис. 7.39.

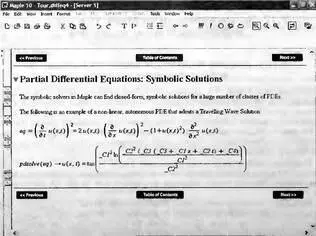
Рис. 7.39. Пример решения дифференциального уравнения в частных производных

Поскольку большая часть новых возможностей Maple 10 в решении дифференциальных уравнений представляет ограниченный интерес для большинства пользователей системой Maple 10 подробное их описание едва ли целесообразно Обзор таких функций и решаемых дифференциальных уравнений можно найти в подразделе Differential Equations раздела What's New справки.

В части средств численного решения дифференциальных уравнении повышена надежность решения жестких систем дифференциальных уравнении и дифференциальных уравнений в частных производных. На рис. 7.40 показан пример решения такого уравнения с выводом результатов в виде анимационного двумерного графика и трехмерного графика, представляющего множество решений в разные моменты времени.

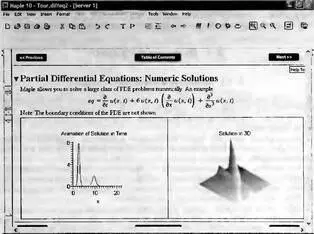
Рис. 7.40. Пример численного решения дифференциального уравнения в частных производных

Эта глава книги посвящена уникальным возможностям системы Maple 9.5/10 в визуализации самых разнообразных вычислений. Рассмотрены возможности и опции двумерной и трехмерной графики, в том числе использующей функциональную окраску. Особое внимание уделено визуализации математических и физических понятий и реализации различных возможностей машинной графики.