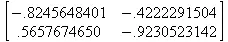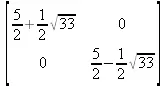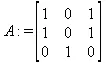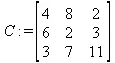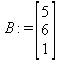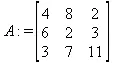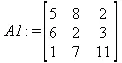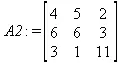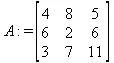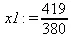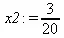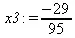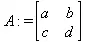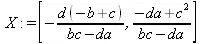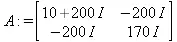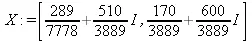Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> eval(V);

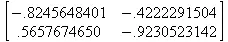
> charpoly(M,p);

> jordan(M);

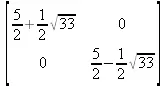
> A:= array([[1,0,1],[1,0,1],[0,1,0]]);

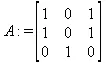
> singularvals(А);

В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.

Одной из самых распространенных задач линейной алгебры является решение систем линейных уравнений. Ниже представлен простой пример составления и решения трех систем линейных уравнений с применением функций, входящих в пакет linalg (файл sle):

> with(linalg):

> C:=matrix(3,3,[[4,8,2],[6,2,3],[3,7,11]]);

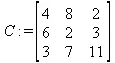
> B:=matrix(3,1, [5,6,1]);

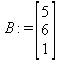
> A:=evalm(C);

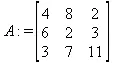
> A1 :=copyinto(В, С, 1, 1);

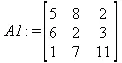
> C:=evalm(A):А2:=copyinto(В,С,1,2);

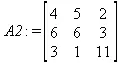
> C:=evalm(A):A3:=copyinto(В,С,1,3);

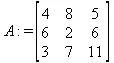
> x1:=det(A1)/det(А);

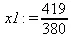
> x2:=det(A2)/det(A);

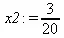
> x3:=det(A3)/det(a);

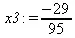
А теперь рассмотрим пример решения матричного уравнения в символьном виде:

> A:=matrix(2,2,[a,b,с,d]);

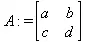
> В:=vector(2, [с,d]);

> X:=linsolve(А,В);

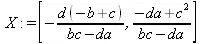
Следующий пример показывает решение более сложной системы линейных уравнений с комплексными коэффициентами:

> А:=matrix(2,2,[[10+200*1,-200*1],[-200*1,170*1]]);

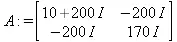
> B:=vector(2, [5,0]);

> X:=multiply(inverse(А),В);

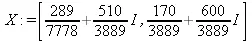
> Digits:=5: convert(eval(X),float);

На этот раз решение получено использованием функций умножения матриц и вычисления обратной матрицы в виде X=А -1∙В, то есть в матричном виде. В конце примера показано преобразование результатов с целью их получения в обычной форме комплексных чисел с частями, представленными в форме чисел с плавающей точкой.

Как видно из описанного, многие вычисления имеют результаты, представляемые в форме матриц. Иногда такие результаты можно наглядно представить графически, например, в виде гистограммы. Она представляет собой множество столбцов квадратного сечения, расположенных на плоскости, образованной осями строк (row) и столбцов (column) матрицы. При этом высота столбцов определяется содержимым ячеек матрицы.

Такое построение обеспечивает графическая функция matnxplot из пакета plots. На рис. 5.1 показано совместное применение этой функции с двумя функциями пакета linafg, формирующими две специальные матрицы Аи В.

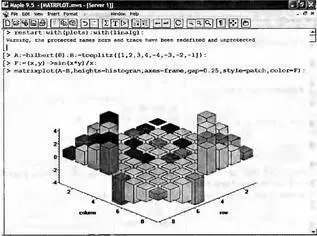
Рис. 6.1. Графическое представление матрицы

На рис. 6.1 показана графическая визуализация матрицы, полученной как разность матриц Aи В. Для усиления эффекта восприятия применяется функциональная закраска разными цветами. Для задания цвета введена процедура F.