Марейн Хавербеке - Выразительный JavaScript
Здесь есть возможность читать онлайн «Марейн Хавербеке - Выразительный JavaScript» весь текст электронной книги совершенно бесплатно (целиком полную версию без сокращений). В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. ISBN: , Жанр: Программирование, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Выразительный JavaScript
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:978-1593275846
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 100
- 1
- 2
- 3
- 4
- 5
Выразительный JavaScript: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Выразительный JavaScript»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Выразительный JavaScript — читать онлайн бесплатно полную книгу (весь текст) целиком
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Выразительный JavaScript», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
Система стилей в HTML называется CSS (Cascading Style Sheets, каскадные таблицы стилей). Таблица стилей – набор стилей в документе. Его можно писать внутри тега :
strong {font-style: italic;color: gray;}
Теперь текст тега strong наклонный и серый.
«Каскадные» означает, что несколько правил комбинируются для получения окончательного стиля документа. В примере на стиль по умолчанию для , который делает текст жирным, накладывается правило из тега , по которому добавляется
font-styleи цвет.Когда значение свойства определяется несколькими правилами, приоритет остаётся у более поздних. Если бы стиль текста в включал правило
font-weight: normal, конфликтующее со стилем по умолчанию, то текст был бы обычный, а не жирный. Стили, которые применяются к узлу через атрибут style, имеют наивысший приоритет.В CSS возможно задавать не только название тегов. Правило для
.abcприменяется ко всем элементам, у которых указан класс “abc”. Правило для \#xyzприменяется к элементу с атрибутом idравным “xyz”(атрибуты idнеобходимо делать уникальными для документа)..subtle {color: gray;font-size: 80%;}#header {background: blue;color: white;}/* Элементы p, у которых указаны классы a и b, а id задан как main */p.a.b#main {margin-bottom: 20px;}Приоритет самых поздних правил работает, когда у правил одинаковая детализация. Это мера того, насколько точно оно описывает подходящие элементы, определяемая числом и видом необходимых аспектов элементов. К примеру, правило для
p.aболее детально, чем правила для pили просто .a, и будет иметь приоритет.Запись
p > a {...}применима ко всем тегам , находящимся внутри тега
p a {...}применимо также ко всем тегам внутри
Селекторы запросов
В этой книге мы не будем часто использовать таблицы стилей. Понимание их работы критично для программирования в браузере, но подробное разъяснение всех их свойств заняло бы 2-3 книги. Главная причина знакомства с ними и с синтаксисом селекторов (записей, определяющих, к каким элементам относятся правила) – мы можем использовать тот же эффективный мини-язык для поиска элементов DOM.
Метод
querySelectorAll, существующий и у объекта document, и у элементов-узлов, принимает строку селектора и возвращает массивоподобный объект, содержащий все элементы, подходящие под него.
Люблю грозу в началемая
Когда весенний первый гром
Как бы резвясяи играя
Грохочет в небе голубом.
function count(selector) {return document.querySelectorAll(selector).length;}console.log(count("p")); // Все элементы
// → 4console.log(count(".animal")); // Класс animal// → 2console.log(count("p .animal")); // Класс animal внутри
// → 2console.log(count("p > .animal")); // Прямой потомок
// → 1В отличие от методов вроде
getElementsByTagName, возвращаемый querySelectorAllобъект не интерактивный. Он не изменится, если вы измените документ.Метод
querySelector(без All) работает сходным образом. Он нужен, если вам необходим один конкретный элемент. Он вернёт только первое совпадение, или null, если совпадений нет.
Расположение и анимация
Свойство стилей
positionсильно влияет на расположение элементов. По умолчанию оно равно static, что означает, что элемент находится на своём обычном месте в документе. Когда оно равно relative, элемент всё ещё занимает место, но теперь свойства topи leftможно использовать для сдвига относительно его обычного расположения. Когда оно равно absolute, элемент удаляется из нормального «потока» документа – то есть, он не занимает место и может накладываться на другие. Кроме того, его свойства leftи topможно использовать для абсолютного позиционирования относительно левого верхнего угла ближайшего включающего его элемента, у которого positionне равно static. А если такого элемента нет, тогда он позиционируется относительно документа.Мы можем использовать это для создания анимации. Следующий документ показывает картинку с котом, которая двигается по эллипсу.
var cat = document.querySelector("img");var angle = 0, lastTime = null;function animate(time) {if (lastTime != null)angle += (time - lastTime) * 0.001;lastTime = time;cat.style.top = (Math.sin(angle) * 20) + "px";cat.style.left = (Math.cos(angle) * 200) + "px";requestAnimationFrame(animate);}requestAnimationFrame(animate);Картинка отцентрирована на странице и ей задана
position: relative. Мы постоянно обновляем свойства topи leftкартинки, чтобы она двигалась.Скрипт использует
requestAnimationFrameдля вызова функции animateкаждый раз, когда браузер готов перерисовывать экран. Функция animateсама опять вызывает requestAnimationFrame, чтобы запланировать следующее обновление. Когда окно браузера (или закладка) активна, это приведёт к обновлениям со скорость примерно 60 раз в секунду, что позволяет добиться хорошо выглядящей анимации.Если бы мы просто обновляли DOM в цикле, страница бы зависла и ничего не было бы видно. Браузеры не обновляют страницу во время работы JavaScript, и не допускают в это время работы со страницей. Поэтому нам нужна
requestAnimationFrame– она сообщает браузеру, что мы пока закончили, и он может заниматься своими браузерными вещами, например обновлять экран и отвечать на запросы пользователя.Наша функция анимации передаётся текущее время через аргументы, которое оно сравнивает с предыдущим (переменная
lastTime), чтобы движение кота было однородным, и анимация работала плавно. Если бы мы просто передвигали её на заданный промежуток на каждом шаге, движение бы запиналось если бы, например, другая задача загрузила бы компьютер.Движение по кругу осуществляется с применением тригонометрических функций
Math.cosи Math.sin. Я кратко опишу их для тех, кто с ними незнаком, так как они понадобятся нам в дальнейшем.Math.cosи Math.sinполезны тогда, когда надо найти точки на круге с центром в точке (0, 0) и радиусом в единицу. Обе функции интерпретируют свой аргумент как позицию на круге, где 0 обозначает точку с правого края круга, затем нужно против часовой стрелки, пока путь диной в 2π (около 6,28) не проведёт нас по кругу. Math.cosсчитает координату по оси x той точки, которая является нашей текущей позицией на круге, а Math.sinвыдаёт координату y. Позиции (или углы) больше, чем 2π или меньше чем 0, тоже допустимы – повороты повторяются так, что a+2π означает тот же самый угол, что и a. 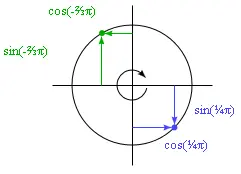
Использование синуса и косинуса для вычисления координат
Интервал:
Закладка:
Похожие книги на «Выразительный JavaScript»
Представляем Вашему вниманию похожие книги на «Выразительный JavaScript» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Выразительный JavaScript» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.










