Виталий Ткаченко - Обратные вызовы в C++

Введем коэффициенты важности для предыдущего примера. Ранжируем требования: считаем, что наименее важным для нас является простота, наиболее важным – безопасность. Результаты приведены в Табл. 9.

Табл. 9. Ранжирование требований

Пересчитаем показатели с учетом коэффициентов важности. Для коэффициентов важности вводим отдельный столбец, где проставляем соответствующие значения. В ячейках в скобках отображаются значения оценки без учета коэффициента, без скобок отображаются новые значения с учетом поправок (Табл. 10).

Табл. 10. Интегральные оценки с учетом коэффициентов важности.

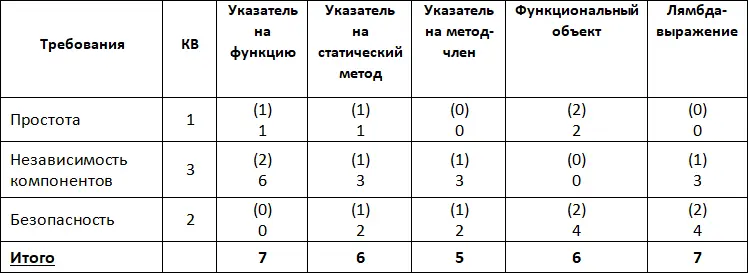
Как видим, после введения коэффициентов важности результаты изменились: теперь максимальное количество балов набирают две реализации – указатель на функцию и лямбда-выражение.

Как мы видели в предыдущем примере, может оказаться, что по результатам расчетов несколько реализаций имеют одинаковое количество балов. В этом случае целесообразно заглянуть в будущее.

Из списка требований выбираем те, которые не актуальны сейчас, но которые, возможно, станут актуальны в последствии. Сводим эти требования в таблицу, аналогично предыдущему примеру, но для числовых значений используем инверсную шкалу: если реализация полностью поддерживает соответствующее требование, выставляем 0, если не поддерживает, то выставляем минимальное отрицательное значение 14 14 Минимальное отрицательное, по модулю оно будет максимальным. . Так, например, если используется трехбалльная шкала, то 0 превращается в -2, 1 превращается в -1, а 2 превращается в 0. Инверсная шкала показывает, насколько сильно новые требования ухудшают текущую интегральную оценку: чем меньше значение 15 15 Мы говорим «меньше», поскольку числа здесь отрицательные. По модулю это значение будет «больше». , тем в большей степени уменьшается текущая оценка.

Далее, полученные оценки суммируются, получившаяся отрицательная интегральная оценка для каждого столбца суммируется с соответствующей текущей оценкой, внося, таким образом, поправки. Из получившихся итоговых значений выбирается реализация, у которой количество балов после коррекции получается наибольшим.

Вернемся к примеру из предыдущего параграфа. Представим, что мы поразмыслили и решили, что в будущем для нас может стать актуальным быстродействие и необходимость реализации C++ API. Сводим эти критерии в таблицу с инверсной шкалой, считаем, что важность этих критериев одинакова. Подсчитываем сумму (Табл. 11).

Табл. 11. Интегральные оценки с инверсной шкалой

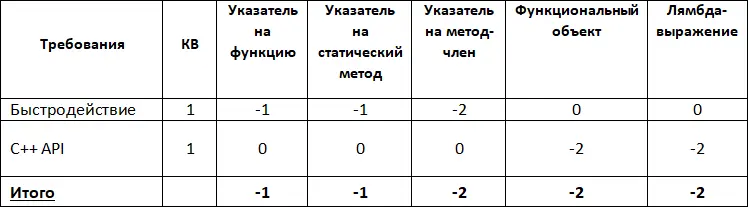
Получившиеся результаты суммируем с результатами, полученными с использованием обычной шкалы (Табл. 12).

Табл. 12. Поправки с учетом инверсной шкалы

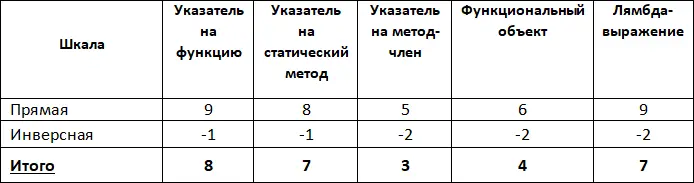
Итак, после внесенных поправок для прогнозных показателей максимальное количество балов набирает указатель на функцию, который рекомендуется к применению.

Может оказаться, что даже после учета прогнозных показателей остаются реализации с одинаковым количеством баллов. В этом случае выбор остается на усмотрение разработчика. Он может, к примеру, взять критерий, который лично для него является более предпочтительным (например, простота), и выбрать реализацию по этому критерию. Или просто выбрать, что называется, первую попавшуюся.

Сравнительный анализ реализаций обратных вызовов необходим для выбора наилучшей в конкретной ситуации. Методика анализа включает в себя выбор объектов, определение критериев сравнения, построение матрицы соответствия, выбор оптимального решения.

Качественный анализ используется, если необходимо выбрать реализацию, оптимальную по какому-нибудь единственному критерию. Если у нас имеется несколько критериев, то необходим количественный анализ, в качестве которого применяется метод интегральных оценок.

Рассмотренные методики подходят не только для исследования обратных вызовов, их можно применять в любых других случаях, когда необходим выбор оптимального архитектурного решения из множества возможных.