Виталий Ткаченко - Обратные вызовы в C++

Полиморфизм . Указатель на метод-член класса поддерживает полиморфизм подтипов (наследование и виртуализация), лямбда-выражения поддерживают специализированный полиморфизм (различный код в зависимости от состава и типов захваченных переменных). Остальные реализации полиморфизм не поддерживают.

Быстродействие . Самым быстродействующим является функциональный объект, практически не отстает от него и лямбда-выражение. Это связано с тем, что их код может встраиваться в точку вызова. Несколько медленнее работают указатели на функцию и на статический метод, поскольку их код выполняется через вызов функции 13 13 При использовании указателей на функцию их код встроить невозможно, потому что заранее неизвестно, какая функция будет использоваться. . Медленнее всего работает указатель на метод-член класса, поскольку ему необходимо обращение к таблице виртуальных функций.

Системный API . Указатель на функцию – единственный способ, с помощью которого можно использовать обратные вызовы при проектировании системных API.

C++ API . Лямбда-выражения не подходят для использования в C++ API: хотя инициатор не требует изменений при модификации исполнителя, но ему требуется перекомпиляция. Не подходят для С++ API также функциональные объекты, поскольку изменение функционального объекта затрагивает как инициатор, так и исполнитель.

Итак, мы построили матрицу соответствия, проанализировали, насколько реализации соответствуют выбранным критериям. Что же выбрать для конкретного случая? Для решения этого вопроса необходимо определить, какой критерий сейчас является наиболее важным, и выбрать реализацию по этому критерию. Так, например, если самым важным является возможность проектирования системного API, то следует выбрать указатели на функцию. Если самым важным является быстродействие, то следует выбрать функциональные объекты. Если самым важным является гибкость, то следует выбрать указатели на член класса.

А как сделать выбор, если нам одновременно важны несколько критериев, причем некоторые из них противоречат друг другу (а чаще всего именно так и происходит)? У нас появляется проблема многокритериального выбора, решить которую позволяет метод интегральных оценок.

По своей сути метод интегральных оценок повторяет качественный анализ, но с одним отличием – в матрице соответствия вместо качественных вводятся количественные оценки. В ячейках матрицы проставляются числовые значения, отражающие, насколько объект анализа поддерживает (другими словами, в какой степени реализует) соответствующее требование. Диапазон возможных значений задается шкалой оценок, которая зависит от точности, которую мы хотим получить. Примеры различных шкал оценок изображены на Рис. 16.

Рис. 16. Шкалы оценки реализуемости требований

Итак, строим матрицу соответствия, в ячейках выставляем числовые оценки, суммируем оценки по столбцам. Реализация, набравшая наибольшее количество баллов, является оптимальной.

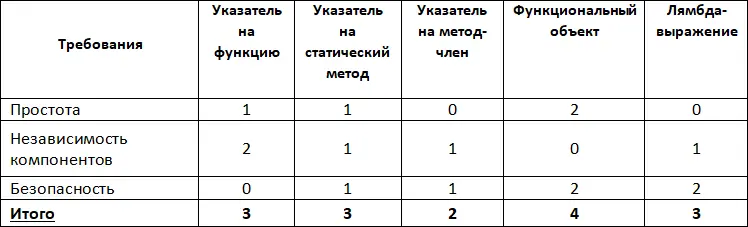
Пример интегральных оценок по трем критериям с использованием трехбалльной шкалы приведен в Табл. 8. Здесь наибольшее количество балов набирает реализация с использованием функционального объекта, которая для конкретного случая является оптимальной.

Табл. 8. Интегральные оценки по трехбалльной шкале

Зачастую оказывается, что некоторые требования являются более важными, чем остальные. Например, быстродействие важно, но в то же время гибкость еще важнее; в свою очередь, безопасность является приоритетным фактором. Чтобы учесть такие ситуации, вводятся коэффициенты важности.

Каждому требованию присваивается коэффициент, который отражает, насколько данное требование является важным для обеспечения качества функционирования системы в конкретном случае. При расчете числовых оценок каждое значение в ячейке таблицы умножается на этот коэффициент; таким образом вносятся поправки в итоговые значения. Целесообразно предварительно ранжировать требования по важности: наименее важному присвоить коэффициент 1, и для каждого требования, более важного, чем предыдущее, увеличивать значение на единицу.