Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

• если В – не константа, то А вообще исключается из таблицы Т, если оно там есть.

Рассмотрим пример выполнения алгоритма.

Пусть фрагмент исходной программы (записанной на языке типа Pascal) имеет вид:

I:= 1 + 1;

I:= 3;

J:= 6*I + I;

Ее внутреннее представление в форме триад будет иметь вид:

1: + (1,1)

2::= (I, ^1)

3::= (I, 3)

4: * (6, I)

5: + (^4, I)

6::= (J, ^5)

Процесс выполнения алгоритма свертки показан в табл. 4.1.

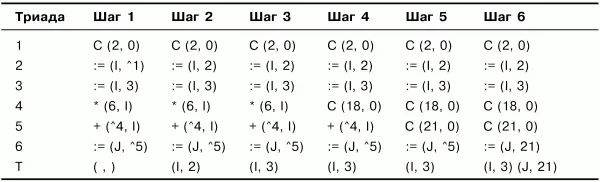
Если исключить особые триады типа C(K,0) (которые не порождают объектного кода), то в результате выполнения свертки получим следующую последовательность триад:

1::= (I, 2)

2::= (I, 3)

3::= (J, 21)

Видно, что результирующая последовательность триад может быть подвергнута дальнейшей оптимизации – в ней присутствуют лишние присваивания, но другие методы оптимизации выходят за рамки данной лабораторной работы (с ними можно познакомиться в [1, 2, 7]).

Алгоритм свертки объектного кода позволяет исключить из линейного участка программы операции, для которых на этапе компиляции уже известен результат. За счет этого сокращается время выполнения, [7]а также объем кода результирующей программы.

Свертка объектного кода, в принципе, может выполняться не только для линейных участков программы. Когда операндами являются константы, логика выполнения программы значения не имеет – свертка может быть выполнена в любом случае. Если же необходимо учитывать известные значения переменных, то нужно принимать во внимание и логику выполнения результирующей программы. Поэтому для нелинейных участков программы (ветвлений и циклов) алгоритм будет более сложным, чем последовательный просмотр линейного списка триад.

Исключение избыточных вычислений (лишних операций) заключается в нахождении и удалении из объектного кода операций, которые повторно обрабатывают одни и те же операнды.

Операция линейного участка с порядковым номером i считается лишней операцией, если существует идентичная ей операция с порядковым номером j, j< i и никакой операнд, обрабатываемый операцией с порядковым номером i, не изменялся никакой другой операцией, имеющей порядковый номер между i и j.

Алгоритм исключения лишних операций просматривает операции в порядке их следования. Так же как и алгоритму свертки, алгоритму исключения лишних операций проще всего работать с триадами, потому что они полностью отражают взаимосвязь операций.

Рассмотрим алгоритм исключения лишних операций для триад.

Чтобы следить за внутренней зависимостью переменных и триад, алгоритм присваивает им некоторые значения, называемые числами зависимости, по следующим правилам:

• изначально для каждой переменной ее число зависимости равно 0, так как в начале работы программы значение переменной не зависит ни от какой триады;

• после обработки i-й триады, в которой переменной А присваивается некоторое значение, число зависимости A (dep(A)) получает значение i, так как значение А теперь зависит от данной i-й триады;

• при обработке i-й триады ее число зависимости (dep(i)) принимается равным значению 1+ (максимальное_из_чисел_зависимости_операндов).

Таким образом, при использовании чисел зависимости триад и переменных можно утверждать, что если i – я триада идентична j-й триаде (j

Алгоритм исключения лишних операций использует в своей работе триады особого вида SAME(j,O). Если такая триада встречается в позиции с номером i, то это означает, что в исходной последовательности триад некоторая триада i идентична триаде j.

Алгоритм исключения лишних операций последовательно просматривает триады линейного участка. Он состоит из следующих шагов, выполняемых для каждой триады:

1. Если какой-то операнд триады ссылается на особую триаду вида SAME(j,0), то он заменяется на ссылку на триаду с номером j (*j).

2. Вычисляется число зависимости текущей триады с номером i, исходя из чисел зависимости ее операндов.

3. Если в просмотренной части списка триад существует идентичная j-я триада, причем j < i и dep(i) = dep(j), то текущая триада i заменяется на триаду особого вида SAME(j,O).

4. Если текущая триада есть присваивание, то вычисляется число зависимости соответствующей переменной.

Рассмотрим работу алгоритма на примере:

D:= D + C*B;