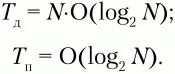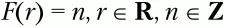Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

2. Сделать текущим узлом дерева корневую вершину.

3. Сравнить имя очередного идентификатора с именем идентификатора, содержащегося в текущем узле дерева.

4. Если имя очередного идентификатора меньше, то перейти к шагу 5, если равно – прекратить выполнение алгоритма (двух одинаковых идентификаторов быть не должно!), иначе – перейти к шагу 7.

5. Если у текущего узла существует левая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе – перейти к шагу 6.

6. Создать новую вершину, поместить в нее информацию об очередном идентификаторе, сделать эту новую вершину левой вершиной текущего узла и вернуться к шагу 1.

7. Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе – перейти к шагу 8.

8. Создать новую вершину, поместить в нее информацию об очередном идентификаторе, сделать эту новую вершину правой вершиной текущего узла и вернуться к шагу 1.

Рассмотрим в качестве примера последовательность идентификаторов Ga, D1, М22, Е, А12, ВС, F. На рис. 1.1 проиллюстрирован весь процесс построения бинарного дерева для этой последовательности идентификаторов.

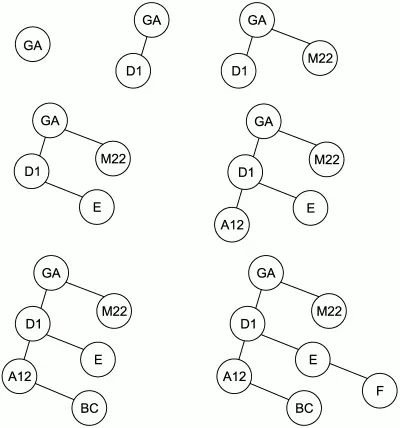
Рис. 1.1. Заполнение бинарного дерева для последовательности идентификаторов.

Поиск элемента в дереве выполняется по алгоритму, схожему с алгоритмом заполнения дерева:

1. Сделать текущим узлом дерева корневую вершину.

2. Сравнить имя искомого идентификатора с именем идентификатора, содержащимся в текущем узле дерева.

3. Если имена совпадают, то искомый идентификатор найден, алгоритм завершается, иначе надо перейти к шагу 4.

4. Если имя очередного идентификатора меньше, то перейти к шагу 5, иначе – перейти к шагу 6.

5. Если у текущего узла существует левая вершина, то сделать ее текущим узлом и вернуться к шагу 2, иначе – искомый идентификатор не найден, алгоритм завершается.

6. Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 2, иначе – искомый идентификатор не найден, алгоритм завершается.

Для данного метода число требуемых сравнений и форма получившегося дерева зависят от того порядка, в котором поступают идентификаторы. Например, если в рассмотренном выше примере вместо последовательности идентификаторов Ga, D1, М22, Е, А12, ВС, F взять последовательность А12, ВС, D1, Е, F, Ga, М22, то дерево выродится в упорядоченный однонаправленный связный список. Эта особенность является недостатком данного метода организации таблиц идентификаторов. Другими недостатками метода являются: необходимость хранить две дополнительные ссылки на левую и правую ветви в каждом элементе дерева и работа с динамическим выделением памяти при построении дерева.

Если предположить, что последовательность идентификаторов в исходной программе является статистически неупорядоченной (что в целом соответствует действительности), то можно считать, что построенное бинарное дерево будет невырожденным. Тогда среднее время на заполнение дерева (Т д) и на поиск элемента в нем (Т п) можно оценить следующим образом [3, 7]:

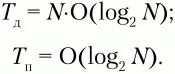
Несмотря на указанные недостатки, метод бинарного дерева является довольно удачным механизмом для организации таблиц идентификаторов. Он нашел свое применение в ряде компиляторов. Иногда компиляторы строят несколько различных деревьев для идентификаторов разных типов и разной длины [1, 2, 3, 7].

В реальных исходных программах количество идентификаторов столь велико, что даже логарифмическую зависимость времени поиска от их числа нельзя признать удовлетворительной. Необходимы более эффективные методы поиска информации в таблице идентификаторов. Лучших результатов можно достичь, если применить методы, связанные с использованием хэш-функций и хэш-адресации.

Хэш-функцией F называется некоторое отображение множества входных элементов R на множество целых неотрицательных чисел Z:

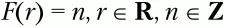
Сам термин «хэш-функция» происходит от английского термина «hash function» (hash – «мешать», «смешивать», «путать»).

Множество допустимых входных элементов R называется областью определения хэш-функции. Множеством значений хэш-функции F называется подмножество М из множества целых неотрицательных чисел Z: