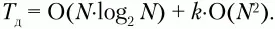Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

Поиск может быть выполнен более эффективно, если элементы таблицы отсортированы (упорядочены) естественным образом. Поскольку поиск осуществляется по имени, наиболее естественным решением будет расположить элементы таблицы в прямом или обратном алфавитном порядке. Эффективным методом поиска в упорядоченном списке из N элементов является бинарный, или логарифмический, поиск.

Алгоритм логарифмического поиска заключается в следующем: искомый символ сравнивается с элементом (N + 1)/2 в середине таблицы; если этот элемент не является искомым, то мы должны просмотреть только блок элементов, пронумерованных от 1 до (N + 1)/2 – 1, или блок элементов от (N + 1)/2 + 1 до N в зависимости от того, меньше или больше искомый элемент того, с которым его сравнили. Затем процесс повторяется над нужным блоком в два раза меньшего размера. Так продолжается до тех пор, пока либо искомый элемент не будет найден, либо алгоритм не дойдет до очередного блока, содержащего один или два элемента (с которыми можно выполнить прямое сравнение искомого элемента).

Так как на каждом шаге число элементов, которые могут содержать искомый элемент, сокращается в два раза, максимальное число сравнений равно 1 + log 2N. Тогда время поиска элемента в таблице идентификаторов можно оценить как T п= O(log 2N). Для сравнения: при N = 128 бинарный поиск требует самое большее 8 сравнений, а поиск в неупорядоченной таблице – в среднем 64 сравнения. Метод называют «бинарным поиском», поскольку на каждом шаге объем рассматриваемой информации сокращается в два раза, а «логарифмическим» – поскольку время, затрачиваемое на поиск нужного элемента в массиве, имеет логарифмическую зависимость от общего количества элементов в нем.

Недостатком логарифмического поиска является требование упорядочивания таблицы идентификаторов. Так как массив информации, в котором выполняется поиск, должен быть упорядочен, время его заполнения уже будет зависеть от числа элементов в массиве. Таблица идентификаторов зачастую просматривается компилятором еще до того, как она заполнена, поэтому требуется, чтобы условие упорядоченности выполнялось на всех этапах обращения к ней. Следовательно, для построения такой таблицы можно пользоваться только алгоритмом прямого упорядоченного включения элементов.

Если пользоваться стандартными алгоритмами, применяемыми для организации упорядоченных массивов данных, то среднее время, необходимое на помещение всех элементов в таблицу, можно оценить следующим образом:

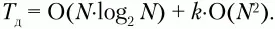
Здесь k – некоторый коэффициент, отражающий соотношение между временами, затрачиваемыми компьютером на выполнение операции сравнения и операции переноса данных.

При организации логарифмического поиска в таблице идентификаторов обеспечивается существенное сокращение времени поиска нужного элемента за счет увеличения времени на помещение нового элемента в таблицу. Поскольку добавление новых элементов в таблицу идентификаторов происходит существенно реже, чем обращение к ним, этот метод следует признать более эффективным, чем метод организации неупорядоченной таблицы. Однако в реальных компиляторах этот метод непосредственно также не используется, поскольку существуют более эффективные методы.

Можно сократить время поиска искомого элемента в таблице идентификаторов, не увеличивая значительно время, необходимое на ее заполнение. Для этого надо отказаться от организации таблицы в виде непрерывного массива данных.

Существует метод построения таблиц, при котором таблица имеет форму бинарного дерева. Каждый узел дерева представляет собой элемент таблицы, причем корневым узлом становится первый элемент, встреченный компилятором при заполнении таблицы. Дерево называется бинарным, так как каждая вершина в нем может иметь не более двух ветвей. Для определенности будем называть две ветви «правая» и «левая».

Рассмотрим алгоритм заполнения бинарного дерева. Будем считать, что алгоритм работает с потоком входных данных, содержащим идентификаторы. Первый идентификатор, как уже было сказано, помещается в вершину дерева. Все дальнейшие идентификаторы попадают в дерево по следующему алгоритму:

1. Выбрать очередной идентификатор из входного потока данных. Если очередного идентификатора нет, то построение дерева закончено.