Алексей Молчанов - Системное программное обеспечение. Лабораторный практикум

• анализ эффективности используемых методов организации таблиц идентификаторов и выводы по проделанной работе.

• Что такое таблица символов и для чего она предназначена? Какая информация может храниться в таблице символов?

• Какие цели преследуются при организации таблицы символов?

• Какими характеристиками могут обладать лексические элементы исходной программы? Какие характеристики являются обязательными?

• Какие существуют способы организации таблиц символов?

• В чем заключается алгоритм логарифмического поиска? Какие преимущества он дает по сравнению с простым перебором и какие он имеет недостатки?

• Расскажите о древовидной организации таблиц идентификаторов. В чем ее преимущества и недостатки?

• Что такое хэш-функции и для чего они используются? В чем суть хэш-адресации?

• Что такое коллизия? Почему она происходит? Можно ли полностью избежать коллизий?

• Что такое рехэширование? Какие методы рехэширования существуют?

• Расскажите о преимуществах и недостатках организации таблиц идентификаторов с помощью хэш-адресации и рехэширования.

• В чем заключается метод цепочек?

• Расскажите о преимуществах и недостатках организации таблиц идентификаторов с помощью хэш-адресации и метода цепочек.

• Как могут быть скомбинированы различные методы организации хеш-таблиц?

• Расскажите о преимуществах и недостатках организации таблиц идентификаторов с помощью комбинированных методов.

В табл. 1.1 перечислены методы организации таблиц идентификаторов, используемые в заданиях.

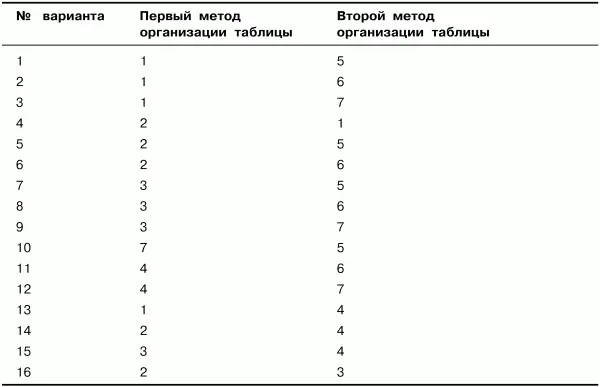
В табл. 1.2 даны варианты заданий на основе методов организации таблиц идентификаторов, перечисленных в табл. 1.1.

В качестве примера выполнения лабораторной работы возьмем сопоставление двух методов: хэш-адресации с рехэшированием на основе псевдослучайных чисел и комбинации хэш-адресации с бинарным деревом. Если обратиться к приведенной выше табл. 1.1, то такой вариант задания будет соответствовать комбинации методов 2 и 7 (в табл. 1.2 среди вариантов заданий такая комбинация отсутствует).

Для хэш-адресации с рехэшированием в качестве хэш-функции возьмем функцию, которая будет получать на входе строку, а в результате выдавать сумму кодов первого, среднего и последнего элементов строки. Причем если строка содержит менее трех символов, то один и тот же символ будет взят и в качестве первого, и в качестве среднего, и в качестве последнего.

Будем считать, что прописные и строчные буквы в идентификаторах различны. [2]В качестве кодов символов возьмем коды таблицы ASCII, которая используется в вычислительных системах на базе ОС типа Microsoft Windows. Тогда, если положить, что строка из области определения хэш-функции содержит только цифры и буквы английского алфавита, то минимальным значением хэш-функции будет сумма трех кодов цифры «0», а максимальным значением – сумма трех кодов литеры «z».

Таким образом, область значений выбранной хэш-функции в терминах языка Object Pascal может быть описана как:

(Ord(0 )+Ord(0 )+Ord(0 ))..(Ord('z')+Ord('z')+Ord('z'))

Диапазон области значений составляет 223 элемента, что удовлетворяет требованиям задания (не менее 200 элементов). Длина входных идентификаторов в данном случае ничем не ограничена. Для удобства пользования опишем две константы, задающие границы области значений хэш-функции:

HASH_MIN = Ord(0 )+Ord(0 )+Ord(0 );

HASH_MAX = Ord('z')+Ord('z')+Ord('z').

Сама хэш-функция без учета рехэширования будет вычислять следующее выражение:

Ord(sName[1]) + Ord(sName[(Length(sName)+1) div 2]) + Ord(sName[Length(sName);

здесь sName – это входная строка (аргумент хэш-функции).

Для рехэширования возьмем простейший генератор последовательности псевдослучайных чисел, построенный на основе формулы F = i-H 1mod Н 2, где Н 1и Н 2– простые числа, выбранные таким образом, чтобы H 1было в диапазоне от Н 2/2 до Н 2. Причем, чтобы этот генератор выдавал максимально длинную последовательность во всем диапазоне от HASH_MIN до HASH_MAX, Н 2должно быть максимально близко к величине HASH_MAX – HASН_МIN + 1. В данном случае диапазон содержит 223 элемента, и поскольку 223 – простое число, то возьмем Н 2= 223 (если бы размер диапазона не был простым числом, то в качестве Н 2нужно было бы взять ближайшее к нему меньшее простое число). В качестве H 1возьмем 127: H 1= 127.