Роберт Мартин - Чистая архитектура. Искусство разработки программного обеспечения

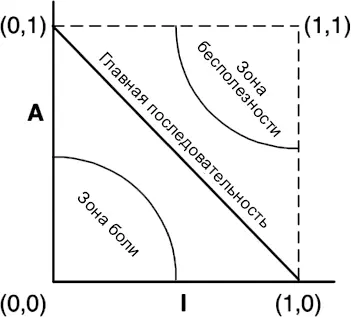
Рис. 14.13.Зоны исключения

Рассмотрим компонент в точке (0, 0). Это очень устойчивый и конкретный компонент. Такие компоненты нежелательны, потому что слишком жесткие. Их нельзя расширить, потому что они неабстрактные, и очень трудно изменить из-за большой устойчивости. Поэтому правильно спроектированные компоненты обычно не должны находиться рядом с точкой (0, 0). Область вокруг точки (0, 0) — это зона исключения, которую называют зоной боли .

Некоторые программные сущности действительно попадают в зону боли. Примером может служить схема базы данных. Схемы баз данных печально известны своей изменчивостью, до предела конкретны и к ним тянется множество зависимостей. Это одна из причин, почему так сложно управлять интерфейсом между объектно-ориентированными приложениями и базами данных и почему изменение схемы обычно связано с большой болью.

Другой пример программного обеспечения, лежащего поблизости от точки (0, 0) — конкретная библиотека вспомогательных функций. Хотя такая библиотека имеет метрику I со значением 1, в действительности она может быть очень негибкой. Возьмем для примера компонент String. Даже при том, что все классы в нем конкретны, он используется настолько широко, что его изменение может породить хаос. Поэтому String — негибкий.

Негибкие компоненты в зоне, окружающей точку (0, 0), безопасны, потому что, скорее всего, не будут изменяться. По этой причине проблемы вызывают только изменчивые программные компоненты, находящиеся в зоне боли. Чем более изменчив компонент, находящийся в зоне боли, тем больше «боли» он доставляет. Фактически изменчивость можно рассматривать как третью ось графика. С этой точки зрения на рис. 14.13 изображена самая болезненная плоскость, где изменчивость = 1.

Рассмотрим компонент рядом с точкой (1, 1). Такие компоненты также нежелательны, потому что они максимально абстрактны и не имеют входящих зависимостей. Они бесполезны. Поэтому данная область так и называется: зона бесполезности .

Программные сущности, находящиеся в этой области, являются своего рода осколками. Часто это оставшиеся абстрактные классы, которые так и не были реализованы. Нам иногда доводится натыкаться на них в системах, где они лежат без использования.

Компонент, находящийся глубоко в зоне бесполезности, должен содержать значительную долю таких сущностей. Очевидно, что присутствие таких бесполезных сущностей нежелательно.

Кажется очевидным, что наиболее изменчивые компоненты должны находиться как можно дальше от зон исключения. Точки, максимально удаленные от обеих зон, лежат на прямой, соединяющей точки (1, 0) и (0, 1). Я называю эту прямую главной последовательностью [32] Автор просит у читателей снисходительности за такое высокопарное заимствование из астрономии. .

Компонент, располагающийся на главной последовательности, не «слишком абстрактный» для своей устойчивости и не «слишком неустойчив» для своей абстрактности. Он не бесполезен и не доставляет особенной боли. От него зависят другие компоненты в меру его абстрактности, и сам он зависит от других в меру конкретности.

Самыми желательными позициями для компонента являются конечные точки главной последовательности. Хорошие архитекторы стремятся разместить подавляющее большинство компонентов в этих точках. Однако, по моему опыту, в большой системе всегда найдется несколько компонентов, недостаточно абстрактных и недостаточно устойчивых. Такие компоненты обладают великолепными характеристиками, когда располагаются на или вблизи главной последовательности.

Мы подошли к последней нашей метрике. Коль скоро желательно, чтобы компонент располагался на или вблизи главной последовательности, можно определить метрику, выражающую удаленность компонента от идеала.

• D [33] В предыдущих публикациях я дал этой метрике имя В’. Теперь я не вижу причин продолжать эту практику. : расстояние. D = | A + I –1| . Эта метрика принимает значения из диапазона [0, 1]. Значение 0 указывает, что компонент находится прямо на главной последовательности. Значение 1 сообщает, что компонент располагается на максимальном удалении от главной последовательности.