У Клоксин - ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

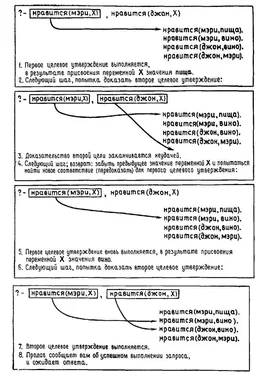
Давайте рассмотрим несколько подробнее, что представляют собой эти дизъюнкты. Как уже было сказано, они состоят из литералов, соединенных друг с другом с помощью дизъюнкции. В общем случае, дизъюнкт выглядит примерно так:

((V # W) # X) # (Y # Z)

где переменные являются литералами. Теперь те же самые рассуждения, которые были сделаны о структуре формулы на верхнем уровне, можно применить к дизъюнктам. Как и выше, скобки не влияют на значение дизъюнкта. Точно так же несуществен и порядок литералов. Таким образом, можно просто сказать, что дизъюнкт – это совокупность литералов (неявно соединенных дизъюнкцией). В последнем примере это будет {V, W, X, Y, Z}

Теперь исходная формула представлена в стандартной форме. Более того, использовавшиеся для преобразования правила не зависят от того, существует или нет интерпретация, при которой формула истинна. Стандартная форма состоит из совокупности дизъюнктов, каждый из которых представляет совокупность литералов. Литерал – это либо атомарная формула, либо отрицание атомарной формулы. Эта форма является достаточно лаконичной, так как в ней опущены логические связки конъюнкций, дизъюнкций и кванторы всеобщности. Но при этом, очевидно, следует помнить о принятых соглашениях. И каждый раз, имея дело со стандартной формой, понимать, где и что в ней опущено. Рассмотрим, что представляет собой стандартная форма некоторых формул (предполагается, что уже выполнены первые пять этапов преобразования). Прежде всего вернемся к уже рассматривавшемуся примеру:

(выходной(Х) # работает(крис,Х)) & (выходной(Х) # (сердитый(крис) # унылый(крис)))

Эта формула порождает два дизъюнкта. Первый дизъюнкт содержит литералы:

выходной(Х), работает(крис,Х)

а второй литералы:

выходной(Х), сердитый(крис), унылый(крис)

Другой пример. Формула

(человек(адам)& человек(ева))&

((человек(Х) # ~мать(Х,Y)) # ~человек(#))

дает три дизъюнкта. Два из них содержат по одному литералу каждый

человек (адам)

и

человек (ева)

Другой содержит три литерала:

человек(Х), ~мать(Х,Y), ~человек(Y)

В заключении этого раздела рассмотрим еще один пример, демонстрирующий все этапы приведения формулы к стандартному виду. Начнем с формулы

all(X, аll(Y,человек(Y) -› почитает(Y,Х) -› король(Х))

утверждающей, что, если все люди относятся с почтением к некоторому человеку, то этот человек является королем. (Для каждого X, если каждый Yявляется человеком, почитающим X, то X– это король). После устранения импликации (этап 1) получаем:

аll(Х,~(аll(Y,~человек(Y) # почитает(Y,Х))) # король(Х))

Перенос отрицания внутрь формулы (этап 2) приводит к следующему:

аll(Х,ехists(Y,человек(Y) & ~почитает(Y,Х)) # король(Х))

Затем, в результате сколемизации (этап 3) формула преобразуется к виду:

аll(Х,(человек(f1(Х)) & ~почитает(f1Х),Х)) # король(Х))

где f1 -сколемовская функция. Теперь производится удаление кванторов всеобщности (этап 4), что приводит к формуле;

(человек(f1(X)) & ~почитает(f1(Х),X)) # король(Х)

Затем формула преобразуется к конъюнктивной нормальной форме (этап 5), в которой конъюнкция не появляется внутри дизъюнктов:

(человек(f1(Х) # король(Х)) & (~почитает(f1(Х), X) # король(Х))

Эта формула содержит два дизъюнкта (этап 6). Первый дизъюнкт имеет два литерала:

человек(f1(Х)), король(Х)

а второй дизъюнкт имеет литералы:

почитает(f1(Х),Х), король(Х)

Очевидно, что для записи формул, представленных в стандартной форме, необходим соответствующий способ. Рассмотрим его. Прежде всего, стандартная форма представляет совокупность дизъюнктов. Договоримся записывать дизъюнкты последовательно один за другим, помня при этом, что порядок записи не имеет значения. В свою очередь, дизъюнкт является совокупностью литералов, часть из которых содержит отрицание, а часть не содержат его. Примем соглашение записывать сначала литералы без отрицания, а затем литералы с отрицанием. Эти две группы литералов будем разделять знаком ':-'. Литералы без отрицания при записи будем отделять друг от друга точкой с запятой (;) (помня, конечно, при этом, что порядок записи литералов в каждой группе неважен), а литералы с отрицанием будем записывать без знака отрицания (~), разделяя литералы запятыми. Запись каждого дизъюнкта будет заканчиваться точкой. При такой форме записи дизъюнкт, содержащий отрицания литералов K, L,… и литералы А, В,… мог бы быть представлен так: