У Клоксин - ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ПРОЛОГ

предложение(Х) означает, что X является последовательностью слов, образующей грамматически правильное предложение.

Таким образом, предполагается, что можно задавать вопросы, подобные следующему:

?- предложение ([the, man, eats, the apple]).

Ответом на этот вопрос будет «да», если «the man eats the apple» является предложением, и «нет» в противном случае.

Представляется довольно неудачным, что мы должны задавать предложения искусственным способом, используя для этого списки атомов языка Пролог. Для более серьезных применений было бы желательно иметь возможность печатать английские предложения на терминале в их естественном виде. В главе 5 было показано, как может быть определен предикат ввестидля того, чтобы преобразовывать напечатанное предложение в список атомов языка Пролог. Очевидно, что мы могли бы использовать этот предикат в нашем синтаксическом анализаторе, чтобы обеспечить естественный способ общения с пользователем программы. Однако здесь мы не будем прибегать к таким «косметическим» средствам, а сконцентрируем внимание на реальных проблемах собственно синтаксического анализа.

В чем состоит проверка последовательности слов на принадлежность множеству правильных предложений? В соответствии с первым правилом грамматики, исходная задача сводится к нахождению словосочетания группа_существительногов начале заданной последовательности слов, а затем словосочетания груп- па_глаголав оставшейся части последовательности. К концу этого процесса мы должны использовать в точности все слова последовательности, ни одним словом больше и ни одним словом меньше. Введем предикаты группа_существительногои группа_глагола, чтобы выразить свойства принадлежности группе существительного и группе глагола:

группа_существительного(Х) означает, что последовательность X является группой существительного. Аналогично, группа_глагола(Х) значит, что последовательность X является группой глагола.

Используя эти предикаты, мы можем дать определение предиката предложение. Последовательность X является предложением, если ее можно разбить на две подпоследовательности Yи Z, где Y– это группа_существительного, Z– группа_глагола. Так как мы представляем последовательности как списки, то у нас уже есть предикат присоединить, выполняющий разбиение списка на два других. Таким образом, можно записать:

предложение(Х):-присоединить(Y,Z,Х), группа_существительного(Y), группа_глагола(Z).

Аналогично

группа_существительного(Х):- присоединить(Y,Z,Х), определитель(Y), существительное(Z).

группа_глагола(Х):- присоединить(Y,Z,Х), глагол(Y), группа_существительного(Z).

группа_глагола(Х):- глагол(Х).

Отметим, что два правила для предиката группа_ глаголапревращаются в два утверждения для нашего предиката, что соответствует двум возможным способам проверки последовательности на принадлежность классу группа_глагола. И наконец, не составляет труда написать утверждения, соответствующие правилам, вводящим слова:

определитель([the]).

существительное([аррlе]).

существительное([man]).

глагол([eats]).

глагол([sings]).

Теперь наша программа завершена. Действительно, эта программа успешно идентифицирует последовательности слов, являющиеся предложениями для приведенной грамматики. Однако, прежде чем считать задачу решенной, следует посмотреть, что в действительности произойдет, когда мы зададим вопрос о некоторой последовательности слов. Рассмотрим утверждение для предиката предложение:

предложение(Х):- присоединить(Y,Z,Х), группа_существительного(Y), группа_глагола(Z).

и следующий вопрос:

?- предложение([the, man, eats, the, apple]).

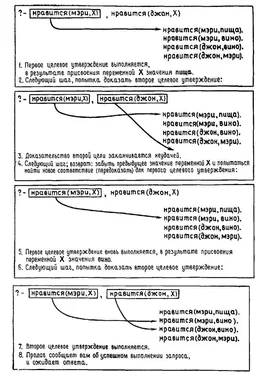
Переменная Xв правиле конкретизируется значением [the, man, eats, the, apple], а переменные Yи Zне будут конкретизированы, так что данная цель будет порождать возможные пары значений для Yи Zтакие, что результат присоединения списка Zк списку Yравен X. С помощью механизма возврата будут порождены все возможные пары, по одной при каждом возврате. Цель группа_ существительногобудет выполняться лишь при условии, что Yдействительно приемлем как группа_существительного. Иначе она не выполняется и присоединить будет вынужден найти другое значение для Y. Так что последовательность выполнения первой части предиката предложениебудет следующей: