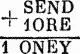Жак Арсак - Программирование игр и головоломок

n дает n ' при переходе p , q ;

n ' дает n при переходе p ', q '.

Как бы то ни было, этого на сей раз недостаточно.

Но это полезно, чтобы увидеть, каким образом 3 играет существенную роль в этом деле…

Общая идея состоит в том, чтобы перепробовать все возможные комбинации, согласующиеся с условием, и сохранить только те из них, которые удовлетворяют предложенной операции.

Головоломка 8.

Пусть даны значения D и E (значения различны). Из них получается Y и то, что «в уме». По этой величине «в уме» получается значение N . Так как N + R + «в уме» = E (плюс, быть может, 10) и так как E известно, то только N можно выбирать произвольно. Кроме того, нужно, чтобы оно отличалось от D , E и Y и нужно, чтобы R , полученное таким образом, отличалось от D , E , Y , N . Если пока все идет хорошо, то вы продолжаете выбор. Если уже возникла невозможность, то вернитесь назад и осуществите другой выбор N . Если никакой выбор для N не оказывается возможным, вернитесь назад и измените выбор E …

Это — одно решение.

Но оно может потребовать много времени. Чтобы выиграть время, ограничьте возможные выборы. Очевидно, что значение SEND ограничено числом 9999, как и MORE, и поэтому значение MONEY не может превосходить 19998. Так как это — число из пяти цифр, то M = 1. Это освобождает вас от испытания 1 для D и E . Если цифра единиц суммы D + E равна 1, то этот набор D и E недопустим.

Поставьте 1 на свое место:

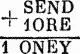
S + 1 + «то, что в уме» дает число, большее девяти. Это возможно только в случае, если мы предположим что «в уме» для S кое-что есть:

S + 2 = 10 + O

(справа буква O, а не цифра ноль).

S + 2 может превосходить 9 только в случае, если S больше 7. Единственные возможные значения — это

S = 8, что дает букве O значение 0,

S = 9, что дает букве O значение 1.

Но 1 уже присвоено букве M. Следовательно, S = 8 и O = 0.

Метод, использованный в этом упражнении, имеет очень широкую область применения. Нужно исследовать все возможности, чтобы выявить те, которые удовлетворяют условию задачи. Мы упорядочиваем их таким образом, чтобы, переходя от одной комбинации к следующей, пересмотреть их все и притом по одному разу.

1. Берем первую комбинацию.

2. Испытываем ее. Если она удовлетворяет требованиям, запоминаем ее значение.

3. Если это — последняя комбинация, то все значения записаны и все кончено.

4. Если не последняя, то переходим к следующей комбинации и повторяем, начиная с пункта 2.

В данном случае — так как мы уже знаем значения букв S, O, M, остается только три еще не определенных значения: D, E, N. Для каждой из них берем постепенно возрастающие значения, изменяя их таким образом, чтобы сначала возрастало N при постоянных D и E. Затем меняется E при постоянном D (а N пробегает все возможные значения). Когда все возможные значения для E испытаны, мы переходим к следующему значению D.

Таким образом, D может принимать 7 значений.

Для каждого из них E может принимать 6 значений.

Для каждой такой пары N может принимать 5 значений.

Отсюда следует, что нужно перепробовать 7 × 6 × 5 = 210 значений, что совершенно не затруднит компьютер…

Головоломка 9.

Будем действовать, как в предыдущей задаче. Но здесь есть некоторая дополнительная информация. В условии участвуют 10 букв:

H E L P T Y O U N G

Так как они имеют значения в виде 10 цифр, где каждая цифра участвует и притом только один раз, то

H + E + L + P + T + Y + O + U + N + G = 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7+ 8 + 9 = 45.

Если вы учтете очевидные значения букв Y, O, H, то вы сможете дать сначала значения каждому из чисел «в уме». Используя тогда соотношения между значениями букв, заданных в зашифрованном сложении, вы сможете получить соотношение между четырьмя буквами и вывести из него, что E нечетно. Отсюда вы быстро выведете, что оно может принимать не более двух значений: 3 и 5.

Испытайте их одно за другим…

Головоломка 10.

Здесь снова используются 10 цифр. Вы знаете их сумму. Она делится на 9. Вы знаете кое-что о сумме цифр результата.

Вы легко сможете заменить это умножение сложением. В нем вы сможете определить все величины «в уме». Вам останется сделать не так уж много попыток…

Головоломка 11.

Эта головоломка намного серьезнее. Если вы пойдете по пути систематических испытаний, то вы рискуете потерять время зря. Есть 9! = 362880 перестановок девяти первых цифр. Не все они подлежат проверке, поскольку крайняя слева цифра не может превосходить 3. Но остается еще очень много возможностей.