Жак Арсак - Программирование игр и головоломок

Вернемся-ка к шахматам. Речи нет о лом, чтобы вы ими занялись; это выше понимания любителя, даже самого талантливого. Но я хочу предложить вам нечто, что все же имеет какое-то отношение к шахматам и одновременно может позволить упражняться в постановке пьесы.

Я представляю шахматную доску на рис. 15 как на экране своего микрокомпьютера в виде квадратной таблицы с 64 полями, которые представлены точками. На шахматной доске в левом верхнем углу расположена черная ладья (помеченная крестом), а в нижнем правом углу — белая ладья (помеченная звездочкой). Тринадцать шашек, помеченных маленькими кружочками, случайным образом расположены на игровом поле. Компьютер перемещает черную ладью ×, а вы — белую ладью *. Каждый игрок на своем ходе передвигает ладью, как при игре в шахматы; только на поля на той же строке или в том же столбце. Можно взять шашку и встать на место, которое она занимала; тогда эта шашка выходит из игры. Можно, взять противоположную ладью, если оказывается возможным попасть на занимаемое ею место. Тогда игра останавливается, и тот, кто взял чужую ладью, и есть победитель. В противном случае игра останавливается, когда больше шашек нет. Тот, кто взял больше шашек, и есть победитель.

Вам необходимо указывать компьютеру, какой именно ход вы хотите сделать. Вы можете, например, отметить строки цифрами, а столбцы — буквами, как на рисунке. Ваш первый ход будет, без сомнения, на H2 или B1…

Стратегия совершенно не очевидна. У вас много возможностей. Не так много, конечно, как в шахматной игре, но достаточно для того, чтобы вам пришлось заняться всерьез, что бы написать программу, которую было бы трудно побить.

Если вы при этом достигли совершенства, почему бы не попробовать ее вариант, который не должен вызывать намного больше затруднений (???): та же задача, но ладьи заменены конями.

*** Игра 26.Могущественная четверка.

Эта игра продается на рынке в другой форме. Она происходит в прямоугольном пространстве с 5 строками и 7 столбцами. Игра ориентирована, у нее есть низ и верх. Игровые позиции суть наинизшие свободные места в каждом столбце. Каждый игрок на своем ходе помещает свой отличительный знак на одно из игровых полей: например, один ставит крестики (+), другой — нолики (0). Первый, кто поставит на одной линии четыре принадлежащих ему знака — либо горизонтально, либо вертикально, либо по диагонали — выигрывает. На рис. 16 будем считать, что нолики при игре ставит тот игрок, чей ход именно сейчас. Если он не сыграет немедленно в пятом столбце, то его противник выиграет следующим ходом. По диагонали, начинающейся у основания четвертого столбца и идущей влево и вверх, есть три нолика, но единственное игровое поле в первом столбце обозначено точкой, и немедленно реализовать продолжение линии поэтому нельзя. Очевидно, что его противник не имеет никакого желания служить ему подставкой при пополнении первого столбца вместо того, чтобы заниматься разыгрыванием мест, допускающих продолжение линии…

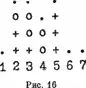
Эту игру, производную от вошек, программировать намного проще, потому что всего полей только 35, и только 7 из них являются игровыми полями на каждом ходе. Это существенно ограничивает работу. В реализованной мною версии ответ микрокомпьютера практически мгновенный (порядка секунды). Я не думаю, что я располагаю программой-чемпионом, я не очень хорошо знаком с атим родом игр…

Я объединил в этой главе несколько игр, которые можно найти на рынке и для которых существует стратегия решения. Как только она становится известной, игра теряет всякий интерес. Единственное связанное с такими играми удовольствие — обнаружить, как с ними покончить. Поэтому напишите программу — это наилучший способ сформулировать выигрышную стратегию, а затем забудьте игру, она вам больше ничего не принесет. И тем хуже, если продавцы этих игр не согласятся со мной… Некоторые из этих игр являются классическими среди информатиков. Я попытался их немного подновить. Многие стратегии могут быть элегантно запрограммированы с помощью рекурсивных процедур, но на языке Бейсик это невозможно. Всегда наступает день, когда фанатики этого языка, такого удобного для первых шагов, начинают понимать его ограниченность… Рекурсивность допустима в языках LSE и Паскаль.