Иван Братко - Программирование на языке Пролог для искусственного интеллекта

9.1. Определите отношение

список( Объект)

для распознавания случаев, когда Объектявляется стандартным прологовским списком.

9.2. Определите отношение принадлежности к списку, используя систему обозначений, введенную в этой разделе: "затем — ничего_не_делать".

9.3. Определите отношение

преобр( СтандСпис, Спис)

для преобразования списков из стандартного представления в систему "затем — ничего_не_делать". Например:

преобр( [а, b], а затем b затем ничего_не_делать)

ответ

9.4. Обобщите отношение преобрна случай произвольного альтернативного представления списков. Конкретное представление задается символом, обозначающим пустой список, и функтором для соединения головы с хвостом. В отношении преобрпридется добавить два новых аргумента:

преобр( СтандСпис, Спис, Функтор, ПустСпис)

Примеры применения этого отношения:

?- пpeoбp( [а, b], L, затем, ничего_не_делать).

L = а затем b затем ничего_не_делать

?- преобр( [а, b, с], L, +, 0).

L = а+(b+(с+0) )

Сортировка применяется очень часто. Список можно отсортировать (упорядочить), если между его элементами определено отношение порядка. Для удобства изложения мы будем использовать отношение порядка

больше( X, Y)

означающее, что X больше, чем Y, независимо от того, что мы в действительности понимаем под "больше, чем". Если элементами списка являются числа, то отношение большебудет, вероятно, определено как

больше( X, Y) :- X > Y.

Если же элементы списка — атомы, то отношение большеможет соответствовать алфавитному порядку между ними.

Пусть

сорт( Спис, УпорСпис)

обозначает отношение, в котором Спис — некоторый список, а УпорСпис — это список, составленный из тех же элементов, но упорядоченный по возрастанию в соответствия с отношением больше. Мы построим три определения этого отношения на Прологе, основанные на трех различных идеях о механизме сортировки. Вот первая идея:

Для того, чтобы упорядочить список Спис, необходимо:

• Найти в Списдва смежных элемента X и Y, таких, что больше( X, Y), и поменять X и Y местами, получив тем самым новый список Спис1; затем отсортировать Спис1.

• Если в Списнет ни одной пары смежных элементов X и Y, таких, что больше( X, Y), то считать, что Списуже отсортирован.

Мы переставили местами 2 элемента X и Y, расположенные в списке "не в том порядке", с целью приблизить список к своему упорядоченному состоянию. Имеется в виду, что после достаточно большого числа перестановок все элементы списка будут расположены в правильном порядке. Описанный принцип сортировки принято называть методом пузырька , поэтому соответствующая прологовская процедура будет называться пузырек.

пузырек( Спис, УпорСпис) :-

перест( Спис, Спис1), !, % Полезная перестановка?

пузырек( Спис1, УпорСпис).

пузырек( УпорСпис, УпорСпис).

% Если нет, то список уже упорядочен

перест( [X, Y | Остаток], [Y, X ) Остаток] ):-

% Перестановка первых двух элементов

больше( X, Y).

перест( [Z | Остаток], [Z | Остаток1] ):-

перест( Остаток, Остаток1). % Перестановка в хвосте

Еще один простой алгоритм сортировки называется сортировкой со вставками. Он основан на следующей идее:

Для того, чтобы упорядочить непустой список L = [X | Хв], необходимо:

(1) Упорядочить хвост Хвсписка L.

(2) Вставить голову X списка L в упорядоченный хвост, поместив ее в такое место, чтобы получившийся список остался упорядоченным. Список отсортирован.

Этот алгоритм транслируется в следующую процедуру вставсортна Прологе:

вставсорт([], []).

вставсорт( [X | Хв], УпорСпис) :-

вставсорт( Хв, УпорХв), % Сортировка хвоста

встав( X, УпорХв, УпорСпис).

% Вставить X на нужное место

встав( X, [Y | УпорСпис], [Y | УпорСпис1]):-

больше( X, Y), !,

встав( X, УпорСпис, УпорСпис1).

встав( X, УпорСпис, [X | УпорСпис] ).

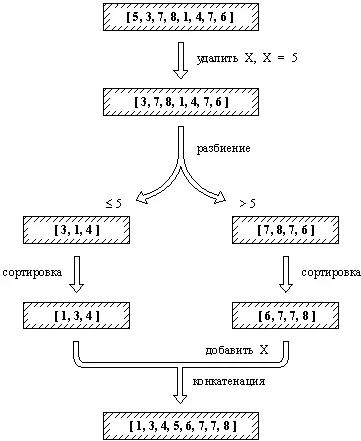
Рис. 9.1. Сортировка списка процедурой быстрсорт.

Процедуры сортировки пузыреки вставсортпросты, но не эффективны. Из этих двух процедур процедура со вставками более эффективна, однако среднее время, необходимое для сортировки списка длиной n процедурой вставсорт, возрастает с ростом n пропорционально n ². Поэтому для длинных списков значительно лучше работает алгоритм быстрой сортировки , основанный на следующей идее (рис. 9.1):