Иван Братко - Программирование на языке Пролог для искусственного интеллекта

• Y-координаты ферзей были различны и

• ферзи не находились на одной диагонали, т.е. расстояние между полями по направлению X не должно равняться расстоянию между ними по Y.

На рис. 4.7 приведен полный текст программы. Чтобы облегчить ее использование, необходимо добавить список-шаблон. Это можно сделать в запросе на генерацию решений. Итак:

?- шаблон( S), решение( S).

решение( [] ).

решение( [X/Y | Остальные ] ) :-

% Первый ферзь на поле X/Y,

% остальные ферзи на полях из списка Остальные

решение( Остальные),

принадлежит Y, [1, 2, 3, 4, 5, 6, 7, 8] ),

небьет( X/Y | Остальные).

% Первый ферзь не бьет остальных

небьет( _, [ ]). % Некого бить

небьет( X/Y, [X1/Y1 | Остальные] ) :-

Y =\= Y1, % Разные Y-координаты

Y1-Y =\= X1-X % Разные диагонали

Y1-Y =\= X-X1,

небьет( X/Y, Остальные).

принадлежит( X, [X | L] ).

принадлежит( X, [Y | L] ) :-

принадлежит( X, L).

% Шаблон решения

шаблон( [1/Y1, 2/Y2, 3/Y3, 4/Y4, 5/Y5, 6/Y6, 7/Y7, 8/Y8]).

Рис. 4.7. Программа 1 для задачи о восьми ферзях.

Система будет генерировать решения в таком виде:

S = [1/4, 2/2, 3/7, 4/3, 5/6, 6/8, 7/5, 8/1];

S = [1/5, 2/2, 3/4, 4/7, 5/3, 6/8, 7/6, 8/1];

S = [1/3, 2/5, 3/2, 4/8, 5/6, 6/4, 7/7, 8/1].

...

4.6. При поиске решения программа, приведенная на рис. 4.7, проверяет различные значения Y-координат ферзей. В каком месте программы задается порядок перебора альтернативных вариантов? Как можно без труда модифицировать программу, чтобы этот порядок изменился? Поэкспериментируйте с разными порядками, имея в виду выяснить, как порядок перебора альтернатив влияет на эффективность программы.

В соответствии с принятым в программе 1 представлением доски каждое решение имело вид

[1/Y1, 2/Y2, 3/Y3, ..., 8/Y8]

так как ферзи расставлялись попросту в последовательных вертикалях. Никакая информация не была бы потеряна, если бы X-координаты были пропущены. Поэтому можно применить более экономное представление позиции на доске, оставив в нем только Y-координаты ферзей:

[Y1, Y2, Y3, ..., Y8]

Чтобы не было нападений по горизонтали, никакие два ферзя не должны занимать одну и ту же горизонталь. Это требование накладывает ограничение на Y-координаты: ферзи должны занимать все горизонтали с 1-й по 8-ю. Остается только выбрать порядок следования этих восьми номеров. Каждое решение представляет собой поэтому одну из перестановок списка:

[1, 2, 3, 4, 5, 6, 7, 8]

Такая перестановка S является решением, если каждый ферзь в ней не находится под боем (список S — "безопасный"). Поэтому мы можем написать:

решение( S) :-

перестановка( [1, 2, 3, 4, 5, 6, 7, 8], S),

безопасный( S).

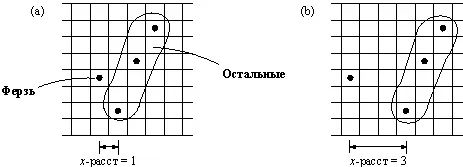
Рис. 4.8. (а) Расстояние по X между Ферзьи Остальныеравно 1. (b) Расстояние по X между Ферзьи Остальныеравно 3

Отношение перестановкамы уже определила в гл. 3, а вот отношение безопасныйнужно еще определить. Это определение можно разбить на два случая:

(1) S — пустой список. Тогда он, конечно, безопасный, ведь нападать не на кого.

(2) S — непустой список вида [Ферзь | Остальные]. Он безопасный, если список Остальные — безопасный и Ферзьне бьет ни одного ферзя из списка Остальные.

На Прологе это выглядит так:

безопасный( []).

безопасный( [Ферзь | Остальные ] :-

безопасный( Остальные),

небьет(Ферзь | Остальные).

В этой программе отношение небьетболее хитрое.

решение( Ферзи) :-

перестановка( [1, 2, 3, 4, 5, 6, 7, 8], Ферзи),

безопасный( Ферзи).

перестановка( [], []).

перестановка( [Голова | Хвост], СписПер) :-

перестановка( Хвост, ХвостПер),

удалить( Голова, СписПер, ХвостПер).

% Вставка головы в переставленный хвост

удалить( А, [А | Список).

удалять( А, [В | Список], [В, Список1] ) :-

удалить( А, Список, Список1).

безопасный( []).

безопасный( [Ферзь | Остальные]) :-

безопасный( Остальные),

небьет( Ферзь, Остальные, 1).

небьет( _, [], _ ).

небьет( Y, [Y1 | СписY], РасстХ) :-

Y1-Y =\= РасстХ,

Y-Y1 =\= РасстХ,

Расст1 is РасстХ + 1,

небьет( Y, СписY, Расст1).