Иван Братко - Программирование на языке Пролог для искусственного интеллекта

верт( отр( точка( X, Y), точка( X, Y1) ) ).

гор( отр( точка( X, Y), точка( X1, Y) ) ).

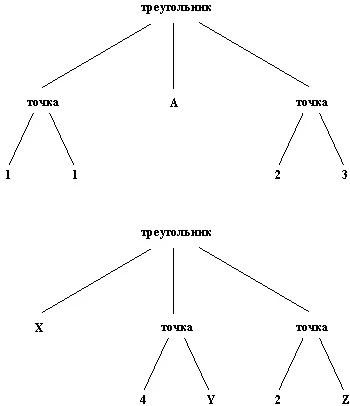
Рис. 2.7.Сопоставление треугольник(( точка( 1, 1), А, точка( 2, 3)) = треугольник( X, точка( 4, Y), точка( 2, Z))

С этой программой возможен такой диалог:

?- верт( отр( точка( 1, 1), точка( 1, 2) ) ).

да

?- верт( отр( точка( 1, 1), точка( 2, Y) ) ).

нет

?- гор( отр( точка( 1, 1), точка( 2, Y) ) ).

Y = 1

На первый вопрос система ответила "да", потому. что цель, поставленная в вопросе, сопоставима с одним из фактов программы. Для второго вопроса сопоставимых фактов не нашлось. Во время ответа на третий вопрос при сопоставлении с фактом о горизонтальных отрезках Y получил значение 1.

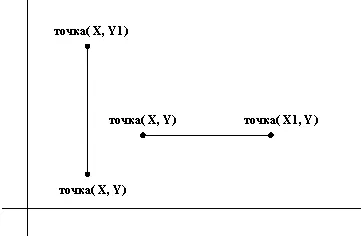
Рис. 2.8. Пример вертикальных и горизонтальных отрезков прямых.

Сформулируем более общий вопрос к программе: "Существуют ли какие-либо вертикальные отрезки, начало которых лежит в точке (2,3)?"

?- верт( отр( точка( 2, 3), P) ).

P = точка( 2, Y)

Такой ответ означает: "Да, это любой отрезок, с концом в точке (2,Y), т.е. в произвольной точке вертикальной прямой x = 2". Следует заметить, что ответ пролог-системы возможно будет выглядеть не так красиво, как только что описано, а (в зависимости от реализации) приблизительно следующим образом:

P = точка( 2, _136)

Впрочем, разница здесь чисто внешняя. В данном случае _136 — это неинициализированная переменная. Имя _136 — законное имя прологовской переменной, которое система построила сама во время вычислений. Ей приходится генерировать новые имена, для того чтобы переименовывать введенные пользователем переменные в программе. Это необходимо по двум причинам: первая — одинаковые имена обозначают в разных предложениях разные переменные; и вторая — при последовательном применении одного и того же предложения используется каждый раз его "копия" с новым набором переменных.

Другим содержательным вопросом к нашей программe является следующий: "Существует ли отрезок, который одновременно и горизонтален в вертикален?"

?- верт( S), гор( S).

S = отр( точка( X, Y), точка( X, Y) )

Такой ответ пролог-системы следует, понимать так: "да, любой отрезок, выродившийся в точку, обладает как свойством вертикальности, так и свойством горизонтальности одновременно". Этот ответ снова получен лишь из сопоставления. Как и раньше, в ответе вместо X и Y могут появиться некоторые имена, сгенерированные системой.

2.3. Будут ли следующие операции сопоставления успешными или неуспешными? Если они будут успешными, то какова будет результирующая конкретизация переменных?

(а) точка( А, В) = точка( 1, 2)

(b) точка( А, В) = точка( X, Y, Z)

(c) плюс( 2, 2) = 4

(d) +( 2, D)= +( E, 2)

(e) треугольник( точка( -1, 0), Р2, Р3) =

треугольник( P1, точка( 1, 0), точка( 0, Y)

Результирующая конкретизация определяет семейство треугольников. Как бы Вы описали это семейство?

2.4. Используя представление отрезков, применявшееся в данной разделе, напишите терм, соответствующий любому отрезку на вертикальной прямой x = 5 .

2.5. Предположим, что прямоугольник представлен термом прямоугольник( P1, P2, P3, Р4), где P — вершины прямоугольника, положительно упорядоченные. Определите отношение

регулярный( R)

которое имеет место, если R — прямоугольник с вертикальными и горизонтальными сторонами.

В главе 1 мы уже видели, что пролог-программу можно понимать по-разному: с декларативной и процедурной точек зрения. В этом и следующем разделах мы рассмотрим более формальное определение декларативного и процедурного смыслов программ базисного Пролога. Но сначала давайте еще раз взглянем на различия между этими двумя семантиками.

Рассмотрим предложение

P :- Q, R.

где P, Q и R имеют синтаксис термов. Приведем некоторые способы декларативной интерпретации этого предложения:

P — истинно, если Q и R истинны.

Из Q и R следует P.

А вот два варианта его "процедурного" прочтения:

Чтобы решить задачу P, сначала реши подзадачу Q, а затем — подзадачу R.

Чтобы достичь P, сначала достигни Q, а затем R.