Иван Братко - Программирование на языке Пролог для искусственного интеллекта

точка( 7, 1) )

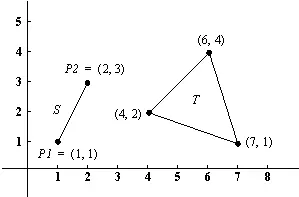
Рис. 2.3. Простые геометрические объекты.

Соответствующее представление этих объектов в виде деревьев приводится на рис. 2.4. Функтор, служащий корнем дерева, называется главным функтором терма.

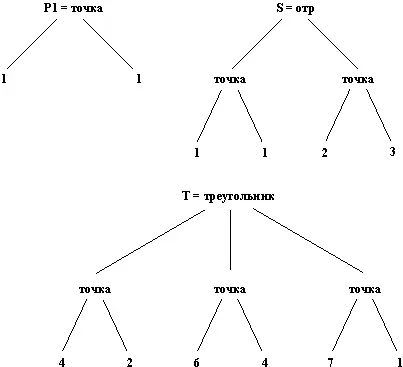
Рис. 2. 4. Представление объектов с рис. 2.3 в виде деревьев.

Если бы в такой же программе фигурировали точки трехмерного пространства, то можно было бы для их представления использовать другой функтор, скажем точка3:

точка3( X, Y, Z)

Можно, однако, воспользоваться одним и тем же именем точкаодновременно и для точек двумерного и трехмерного пространств и написать, например, так:

точка( XI, Y1) и точка( X, Y, Z)

Если одно и то же имя появляется в программе в двух различных смыслах, как в вышеупомянутом примере с точкой, то пролог-система будет различать их по числу аргументов и интерпретировать это имя как два функтора: один — двухаргументный; второй — трех. Это возможно потому, что каждый функтор определяется двумя параметрами:

(1) именем, синтаксис которого совпадает с синтаксисом атомов;

(2) арностью — т.е. числом аргументов.

Как уже объяснялось, все структурные объекты в Прологе — это деревья, представленные в программе термами. Рассмотрим еще два примера, чтобы показать, насколько удобно сложные объекты данных представляются с помощью прологовских термов. На рис. 2.5 показана древовидная структура, соответствующая арифметическому выражению

(a + b)*(c - 5)

В соответствии с введенным к настоящему моменту синтаксисом, такое выражение, используя символы *, + и - в качестве функторов, можно записать следующим образом:

*( +( a, b), -( c, 5))

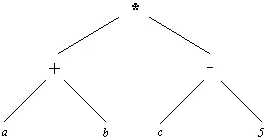
Рис. 2.5. Древовидная структура, соответствующая арифметическому выражению (a + b)*(c - 5) .

Это, конечно, совершенно правильный прологовский терм, однако это не та форма, которую нам хотелось бы иметь, при записи арифметических выражений. Хотелось бы применять обычную инфиксную запись, принятую в математике. На самом деле Пролог допускает использование инфиксной нотации, при которой символы *, + и - записываются как инфиксные операторы. Детали того, как программист может определять свои собственные операторы, мы приведем в гл. 3.

В качестве последнего примера рассмотрим некоторые простые электрические цепи, изображенные на рис. 2.6. В правой части рисунка помещены древовидные представления этих цепей. Атомы r1, r2, r3и r4 — имена резисторов. Функторы пари послобозначают соответственно параллельное и последовательное соединение резисторов. Вот соответствующие прологовские термы:

посл( r1, r2)

пар( r1, r2)

паp( rl, пap( r2, r3))

пар( r1, посл( пар( r2, r3), r4))

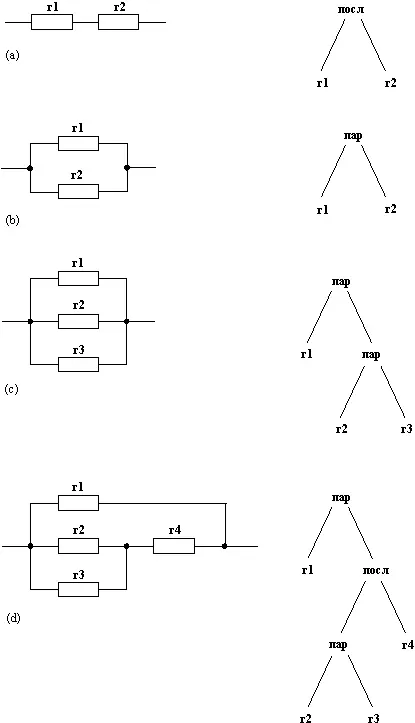
Рис. 2.6. Некоторые простые электрические цепи и их представление: (а) последовательное соединение резисторов r1 и r2; (b) параллельное соединение двух резисторов; (с) параллельное соединение трех резисторов; (d) параллельное соединение r1 и еще одной цепи.

2.1. Какие из следующих выражений представляют собой правильные объекты в смысле Пролога? Что это за объекты (атомы, числа, переменные, структуры)?

(а) Диана

(b) диана

(с) 'Диана'

(d) _диана

(e) 'Диана едет на юг'

(f) едет( диана, юг)

(g) 45

(h) 5( X, Y)

(i) +( север, запад)

(j) три( Черные( Кошки))

2.2. Предложите представление для прямоугольников, квадратов и окружностей в виде структурных объектов Пролога. Используйте подход, аналогичный приведенному на рис. 2.4. Например, прямоугольник можно представить четырьмя точками (а может быть, только тремя точками). Напишите несколько термов конкретных объектов такого типа с использованием предложенного вами представления.

В предыдущем разделе мы видели, как используются термы для представления сложных объектов данных. Наиболее важной операцией над термами является сопоставление . Сопоставление само по себе может производить содержательные вычисления.