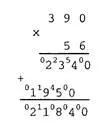В Камаев - Технологии программирования

begin

{ Расчет двух различных корней }

x1:= (-b) — Sqrt(d)/(2.0*a);

х2:= (-b) + Sqrt(d)/(2.0*a);

Write ('два различных корня x1 = ', x1:10:4);

WriteLn (' х2 = ', х2:10:4);

end;

if ((d >= -1e-6) and (d <= 1e-6))

then

WriteLn ('два равных корня х = ', (-b)/(2.0*a):10:4);

if d < -1e-6 then

WriteLn ('уравнение не имеет решения');

end;

if ((Abs(a) <= 1e-6) and (Abs(b) > 1e-6))

then

begin

{ Решение линейного уравнения }

x1:= — c/b;

WriteLn ('уравнение линейное х = ', x1:10:4);

end;

if ((Abs(a) <= 1e-6) and (Abs(b) <= 1e-6 and (Abs(c) > 1e-6))

then

WriteLn ('Нет решения');

if ((Abs(a) <= 1e-6 and (Abs(b) <= 1e-6 and (Abs(c) <= 1e-6))

then

begin

Write ('Бесчисленное множество решений',

'уравне');

WriteLn ('ния (корни — любые числа)');

end;

WriteLn;

Write ('Для завершения программы нажмите');

WriteLn ('любую клавишу…');

repeat until KeyPressed; { Цикл ожидания нажатия любой клавиши }

end.

В качестве примера приводится учебная работа, выполненная одним из обучаемых. Работа была оформлена на отдельных листах формата A4. Курсивом выделены пояснения авторов учебника, которые были дополнительно ими внесены в текст работы.

Страница 1 (без нумерации) представляет собой титульный лист с наименованием: "ЗАДАНИЕ НА СОСТАВЛЕНИЕ СТРУКТУРИРОВАННОГО АЛГОРИТМА".

Страница 2 содержит постановку задачи и набор тестов, составленных до разработки алгоритма процесса.

Шаг 1. ПОСТАНОВКА ЗАДАЧИ

Составить алгоритм умножения двух положительных чисел с произвольным (до ста) количеством цифр. Цифры сомножителей и результата должны находиться в одномерных массивах. Разрядность результата не должна превышать 100 цифр.

Шаг 2. НАБОР ТЕСТОВ, СОСТАВЛЕННЫХ ДО РАЗРАБОТКИ АЛГОРИТМА ПРОЦЕССА

Пусть предельная разрядность сомножителей равна трем цифрам, а результата — четырем. Аналогично приведенному образцу умножения чисел 391*56 = 21896 (переполнение) были составлены тесты: 23*132 = 3036; 111*11 = 1221; 999*99 = 98901 (переполнение); 00*000 = 0; 1*0 = 0.

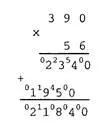
Алгоритм умножения обычно изучался в младших классах школы по маршрутному описанию процесса счета. Из-за теоретической огромности числа маршрутов большинство со школьной скамьи не знает процесса умножения при нулевых сомножителях!

Страница 3 содержит результаты анализа выходной и входной информации вычислительного процесса со структурами данных. Рациональность избранной структуры данных в значительной мере определяет рациональность алгоритма.

Шаг 3. АНАЛИЗ ВЫХОДНОЙ И ВХОДНОЙ ИНФОРМАЦИИ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА

Анализ выходной и входной информации начинается с рассмотрения модели "черного" ящика, показанной на рис. 5.3.

Program MultNumbers;

{Расчет произведения двух чисел}

uses

Crt;

const

Digits = 100; {Число цифр в числах}

type

TNumber = record

D: array[1..Digits] of Byte;

{B D[1] находится младший разряд числа}

N: word; {Число разрядов в числе от 1 до Digits}

end;

var

C1: TNumber; {Первый сомножитель}

C2: TNumber; {Второй сомножитель}

R: TNumber; {Результат умножения}

Error: boolean; {True — ошибка переполнения}

Макет экрана со строками диалога программы приведен на рис. 5.17. Вместо трех последних строк возможен вывод: "Ошибка переполнения".

Страница 4 содержит наглядное изображение процесса преобразования входных данных обобщающего теста или тестов в выходные данные со всеми внутренними данными и/или трассу выполнения обобщающего теста или тестов. Обобщающий тест или тесты составляются на основе тестов страницы 2 и при минимальном количестве тестов охватывает все маршруты процесса вычислений. Наглядность изображения изменений всех данных способствует упрощению процесса разработки алгоритма. Рациональность избранной структуры данных в значительной мере определяет рациональность алгоритма.

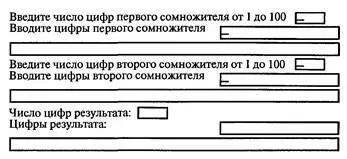
Рис. 5.17. Макет экрана со строками диалога программы

Шаг 4. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ ПРОЦЕССА ПРЕОБРАЗОВАНИЯ ВХОДНЫХ ДАННЫХ ОБОБЩАЮЩЕГО ТЕСТА В ВЫХОДНЫЕ