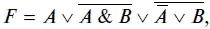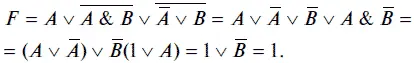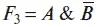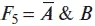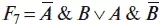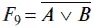Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:
1. Коммутативный закон: A & B = B & A; A ∨ B = B ∨ A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ∨ (B ∨ C) = (A ∨ B) ∨ C.
3. Дистрибутивный закон: A & (B ∨ C) = (A & B) ∨ (A & C).
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (⇒), эквиваленция (⇔)
Выполним преобразование, например, логической функции
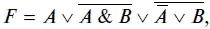
применив соответствующие законы алгебры логики.
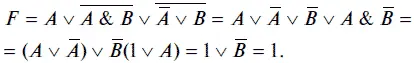
4.3. Логические функции и таблицы истинности
Соотношения между логическими переменными и логическими функциями в алгебре логики можно отобразить также с помощью соответствующих таблиц, которые носят название таблиц истинности. Таблицы истинности находят широкое применение, поскольку наглядно показывают, какие значения принимает логическая функция при всех сочетаниях значений ее логических переменных. Таблица истинности состоит из двух частей. Первая (левая) часть относится к логическим переменным и содержит полный перечень возможных комбинаций логических переменных А, В, С… и т. д. Вторая (правая) часть этой таблицы определяет выходные состояния как логическую функцию от комбинаций входных величин.
Например, для логической функции F = A v B v C (дизъюнкции) трех логических переменных А, В, и С таблица истинности будет иметь вид, показанный на рис. 4.1. Для записи значений логических переменных и логической функции данная таблица истинности содержит 8 строк и 4 столбца, т. е. число строк для записи значений аргументов и функции любой таблицы истинности будет равно 2 n, где п – число аргументов логической функции, а число столбцов равно п + 1.
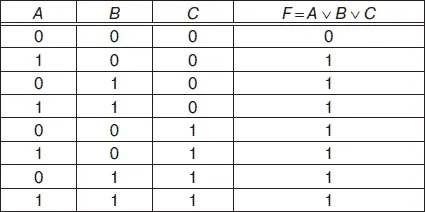
Рис. 4.1. Таблица истинности для логической функции F = A v В v С
Таблицу истинности можно составить для любой логической функции, например, на рис. 4.2 приведена таблица истинности логической функции F = A ⇔ B ⇔ C (эквиваленции).
Логические функции имеют соответствующие названия. Для двух двоичных переменных существует шестнадцать логических функций, названия которых приведены ниже. На рис. 4.3 представлена таблица, в которой приведены логические функции F 1, F 2, F 3 , … , F 16 двух логических переменных A и В.
Функция F 1= 0 и называется функцией константы нуля, или генератора нуля.
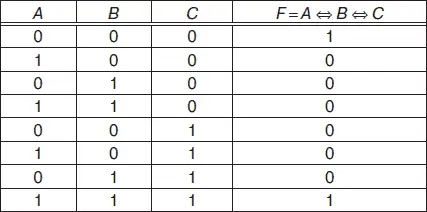
Рис. 4.2. Таблица истинности для логической функции F = A ⇔ B ⇔ C
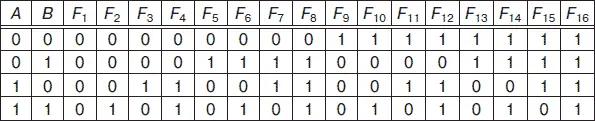
Рис. 4.3. Логические функции F 1, F 2, F 3,… F 16двух аргументов А и В
Функция F 2= A & B называется функцией конъюнкции.
Функция
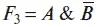
называется функцией запрета по логической переменной А.
Функция F 4= А называется функцией повторения по логической переменной А.
Функция
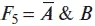
называется функцией запрета по логической переменной В.
Функция F 6= В называется функцией повторения по логической переменной В.
Функция
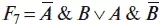
называется функцией исключающее «ИЛИ».
Функция F 8= A v В называется функцией дизъюнкции.
Функция
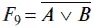
называется функцией Пирса.
Читать дальше
Конец ознакомительного отрывка
Купить книгу