Владимир Яшин - Информатика - аппаратные средства персонального компьютера

где Р – порядок числа,

т. е. вместо основания системы счисления 10 пишут букву Е, вместо запятой – точку, и знак умножения не ставится. Таким образом, число 15,5 в формате с плавающей запятой и линейной записи (компьютерное представление) будет записано в виде: 0.155Е2; 1.55Е1; 15.5Е0; 155.0Е-1; 1550.0Е-2 и т.д.

Независимо от системы счисления любое число в форме с плавающей запятой может быть представлено бесконечным множеством чисел. Такая форма записи называется ненормализованной. Для однозначного представления чисел с плавающей запятой используют нормализованную форму записи числа, при которой мантисса числа должна отвечать условию

где |А| — абсолютное значение мантиссы числа.

Условие (2.9) означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля, или, другими словами, если после запятой в мантиссе стоит не нуль, то число называется нормализованным. Так, число 15,5 в нормализованном виде (нормализованная мантисса) в форме с плавающей запятой будет выглядеть следующим образом: 0,155 · 10 2, т. е. нормализованная мантисса будет A = 0,155 и порядок Р = 2, или в компьютерном представлении числа 0.155Е2.

Числа в форме с плавающей запятой имеют фиксированный формат и занимают в памяти компьютера четыре (32 бит) или восемь байт (64 бит). Если число занимает в памяти компьютера 32 разряда, то это число обычной точности, если 64 разряда, то это число двойной точности. При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, мантиссы и порядка. Количество разрядов, которое отводится под порядок числа, определяет диапазон изменения чисел, а количество разрядов, отведенных для хранения мантиссы, – точность, с которой задается число.

При выполнении арифметических операций (сложение и вычитание) над числами, представленными в формате с плавающей запятой, реализуется следующий порядок действий (алгоритм) :

1) производится выравнивание порядков чисел, над которыми совершаются арифметические операции (порядок меньшего по модулю числа увеличивается до величины порядка большего по модулю числа, мантисса при этом уменьшается в такое же количество раз);

2) выполняются арифметические операции над мантиссами чисел;

3) производится нормализация полученного результата.

Поясним сказанное выше на примерах.

Произведем сложение двух чисел 0,5 · 10 2и 0,8 · 10 3в формате с плавающей запятой.

Решение.

Проведем выравнивание порядков и сложение мантисс 0,05 · 10 3+ 0,8 · 10 3= 0,85 · 10 3. Полученная мантисса 0,85 является нормализованной, так как удовлетворяет условию (2.9).

Произведем сложение двух чисел 0,1 · 2 2и 0,1 · 2 3в формате с плавающей запятой.

Решение.

Проведем выравнивание порядков и сложение мантисс: 0,01 · 2 3+ 0,1 · 2 3= 0,11 · 2 3. Полученная мантисса 0,11 является нормализованной, так как удовлетворяет условию (2.9).

1. Перевести числа, записанные в римской системе счисления, в числа десятичной системы счисления:

a) XL; б) СХХХ; в) CDXXVIII; г) CMLXXVI; д) MCMLII; е) MMV.

2. Используя программу MS Excel, реализовать автоматический перевод чисел из десятичной системы счисления в римскую.

3. Создать и заполнить все ячейки следующей таблицы, используя табличный процессор MS Excel.

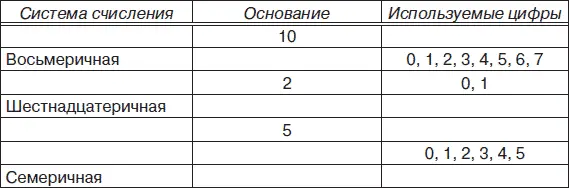
4. Используя формулы (2.1) —(2.6) записать в развернутом виде числа:

a) K 10= 12355; б) К 8= 321476; в) К 2= 101110011;

г) K 16= 143D5; е) K 10= 769,314; ж) К 8= 0,1734;

з) K 2= 100101,011; и) K 16= ЗА1,5С1.

5. Заполнить все строки следующей таблицы.

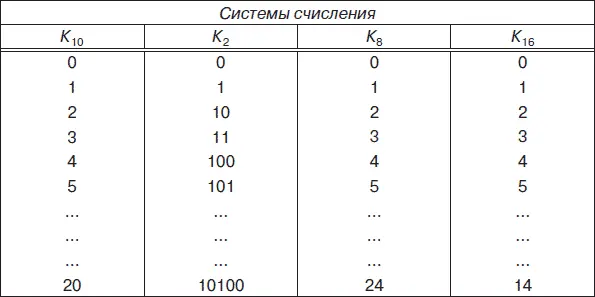
6. Правильно ли записаны числа в соответствующих системах счисления:

а) К 2= 100200; б) K 16= CD1; в) K 10= F,345; г) K 8= -122453?

7. Какие из чисел 3D7 16, 10010111 2, 375 8и 13424 5являются наибольшим и наименьшим?

8. Перевести числа 234 10, 1000 10, 30,75 10, 9,8 10в двоичную, восьмеричную и шестнадцатеричную системы счисления.

9. Перевести числа 10001 2, 1010,01 2, 111111 2, 1001110,011 2в десятичную, восьмеричную и шестнадцатеричную системы счисления.