Владимир Большаков - КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия

При построении тороида вращается только контур в эскизе. К получившейся поверхности добавляется слой материала. В результате получается тонкостенный элемент — элемент с отверстием вдоль оси вращения. Параметры тонкой стенки могут быть заданы.

При создании элемента вращения можно задать направление и угол вращения эскиза.

Построение 3D-моделей простых тел вращения по их параметрам не является для большинства очень увлекательной задачей из-за ее простоты. Рассмотрим примеры.

Условие. Построить модель сферы, у которой сечение, отстоящее на 12 мм от центра, имеет радиус, равный 8 мм.

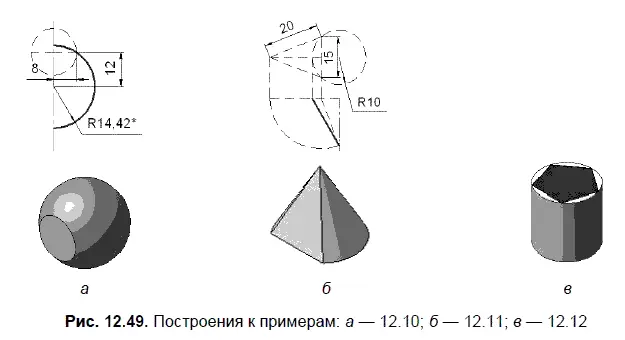
Решение. На рис. 12.49, а показаны вспомогательные построения, которые необходимо выполнить в эскизе для построения дуги указанного знаком «*» радиуса, а также модель сферы с заданным сечением.

Условие. Построить модель цилиндра высотой 25 мм, описанного вокруг правильной пятиугольной призмы. Основание призмы описано вокруг окружности с радиусом 10 мм.

Решение. На рис. 12.49, б показан цилиндр и пятиугольник, который первоначально строится в эскизе, после чего вокруг него описывается окружность. Очевидно, что далее достаточно выдавить эскиз на заданное расстояние.

Условие. Построить модель конуса, у которого радиус основания равен 10 мм, а сечение, проходящее через вершину конуса и хорду длиной 15 мм, имеет боковую сторону длиной 20 мм.

Решение. На рис. 12.49, в показан эскиз, в котором первоначально строится сечение по заданным параметрам. Поворот сечения вокруг хорды позволяет найти положение вершины конуса. Далее изображается отрезок (образующая), вращение которого вокруг оси позволяет создать модель конуса. Показанный на рис. 12.49, в конус содержит заданное в условии сечение.

В последующих примерах определим основные параметры касающихся геометрических тел, которые позволят, используя рассмотренные ранее приемы, построить соответствующие модели.

Условие. Определить высоту тетраэдра, описанного вокруг цилиндра с диаметром и высотой 10 мм. Для построений использовать проекции вспомогательного тетраэдра.

Решение представлено на рис. 12.50.

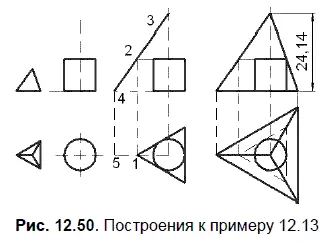
1. Используя команду Многоугольник, опишите вокруг окружности правильный треугольник.

2. Из вершины треугольника проведите отрезок 12. Точка 2 должна быть построена на уровне верхней грани цилиндра.

3. Через точку 2 проведите отрезок 34, параллельный боковому ребру вспомогательного тетраэдра. Концы отрезка необходимо выровнять до соответствующих осей.

4. Постройте вспомогательный отрезок 45. Точка 5 должна быть расположена на продолжении горизонтальной оси, проходящей через центр окружности.

5. Постройте фронтальную и горизонтальную проекции тетраэдра. Нанесите размер, определяющий высоту тетраэдра.

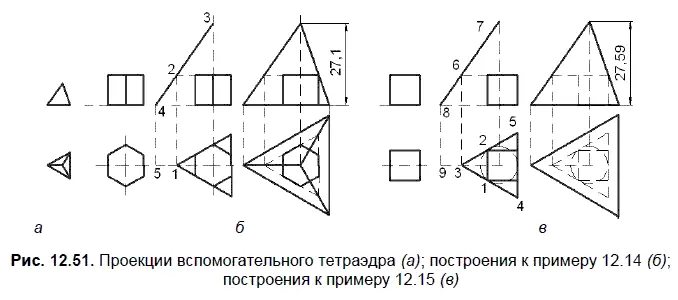
Условие. Определить высоту тетраэдра, описанного вокруг правильной шестиугольной призмы. Расстояние между противоположными гранями призмы — 10 мм. Для построений использовать проекции вспомогательного тетраэдра (рис. 12.51, а ).

Решение приведено на рис. 12.51, б.

1. Через точки 1 и 2 проведите отрезок 34, параллельный боковому ребру вспомогательного тетраэдра. Концы отрезка необходимо выровнять до соответствующих осей. Постройте треугольник, описанный вокруг горизонтальной проекции призмы.

2. Из вершины треугольника проведите отрезок 12. Точка 2 должна быть построена на уровне верхней грани призмы.

3. Через точку 2 проведите отрезок 34, параллельный боковому ребру вспомогательного тетраэдра. Концы отрезка необходимо выровнять до соответствующих осей.

4. Постройте вспомогательный отрезок 45. Точка 5 должна быть расположена на продолжении горизонтальной оси, проходящей через центр шестиугольника.