Неопределенность состояния системы характеризуется информационной энтропией.
Информационная энтропия — это мера неопределенности или непредсказуемости информации о системе.
Пусть система реагирует на некоторое воздействие событием x, которое может иметь n возможных состояний xi , (i=1,…,n), а p(i) – вероятность конкретного состояния xi . Тогда, согласно классической формуле, информационная энтропия этой системы будет равна:
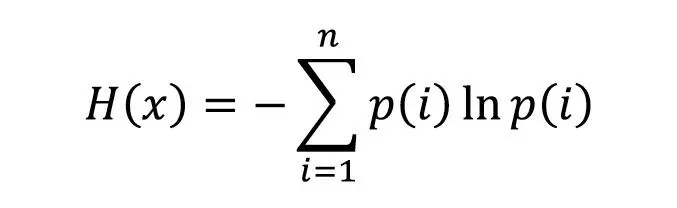
Использование энтропийных методов при проектировании новых моделей бизнес-процессов получило уже достаточно широкое распространение. Исследована информационная энтропия типовых моделей бизнес-процессов (последовательный, параллельный, цикл)[86], предложен метод сравнительной оценки существующей и проектируемой моделей бизнес-процесса на основе энтропии результатов их имитационного моделирования[87]. В книге Ивери Прангишвили рассмотрены некоторые энтропийные модели бизнес-процессов предприятий[88]. В работе[89] исследована адаптивность сетевых организационных структур на базе энтропии сети. Все эти методы опираются на свойства информационной энтропии:
1. Неотрицательность H(x)≥0.
2. Ограниченность H(x)≤ln n, где n – количество возможных состояний системы.
3. Если x, y независимы, то H(xy)=H(x)+H(y).
4. Если x, y зависимы, то H(xy)=H(x)+H(y|x)=H(y)+H(x|y).
Первое и второе из перечисленных свойств позволяют построить метрику эффективности транзакционного (управленческого) процесса на основе энтропии его параметра. Пусть µ – некий характерный параметр процесса (например, время выполнения) и в зависимости от различных случайных факторов этот параметр может принимать значения μi, i=1, … , n, где n – количество возможных результатов процесса. Если за период времени t процесс выполнялся N раз, предлагаемая метрика будет иметь вид:
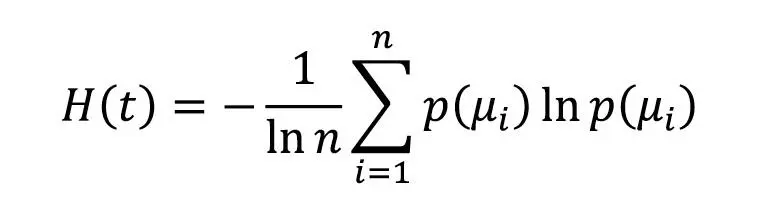
где p(μi ) – доля процессов с исходом μi в общем числе процессов, выполненных за указанный период времени.
Известно, что максимальным значением энтропии H(x)=ln n обладает равномерно распределенная случайная величина, а минимальным H(x)=0 величина, которая всегда принимает одно и то же значение (т.е. постоянная). Соответственно, состоянию наименьшей информированности о бизнес-процессе, когда все его возможные результаты равновероятны, соответствует значение H(t)=1, состоянию полной определенности, когда возможен только один результат, значение H(t)=0. Тем самым фиксируя изменение значения H(t) до, во время и после внедрения ИС можно судить о степени ее эффективности.
Отметим, что введение нормирующего множителя 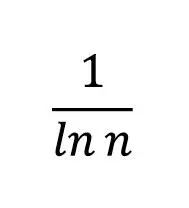 в формулу делает метрику универсальной и позволяет использовать ее как для общей оценки зрелости исследуемого бизнес-процесса (чем ближе его метрика к 0, тем более предсказуемы его исходы), так и даже для сравнения эффективности различных процессов. Для лучшего понимания введенной метрики рассмотрим таблицу 5.1, в строках которой приведено количество исходов с результатом μi для различных опытов.
в формулу делает метрику универсальной и позволяет использовать ее как для общей оценки зрелости исследуемого бизнес-процесса (чем ближе его метрика к 0, тем более предсказуемы его исходы), так и даже для сравнения эффективности различных процессов. Для лучшего понимания введенной метрики рассмотрим таблицу 5.1, в строках которой приведено количество исходов с результатом μi для различных опытов.

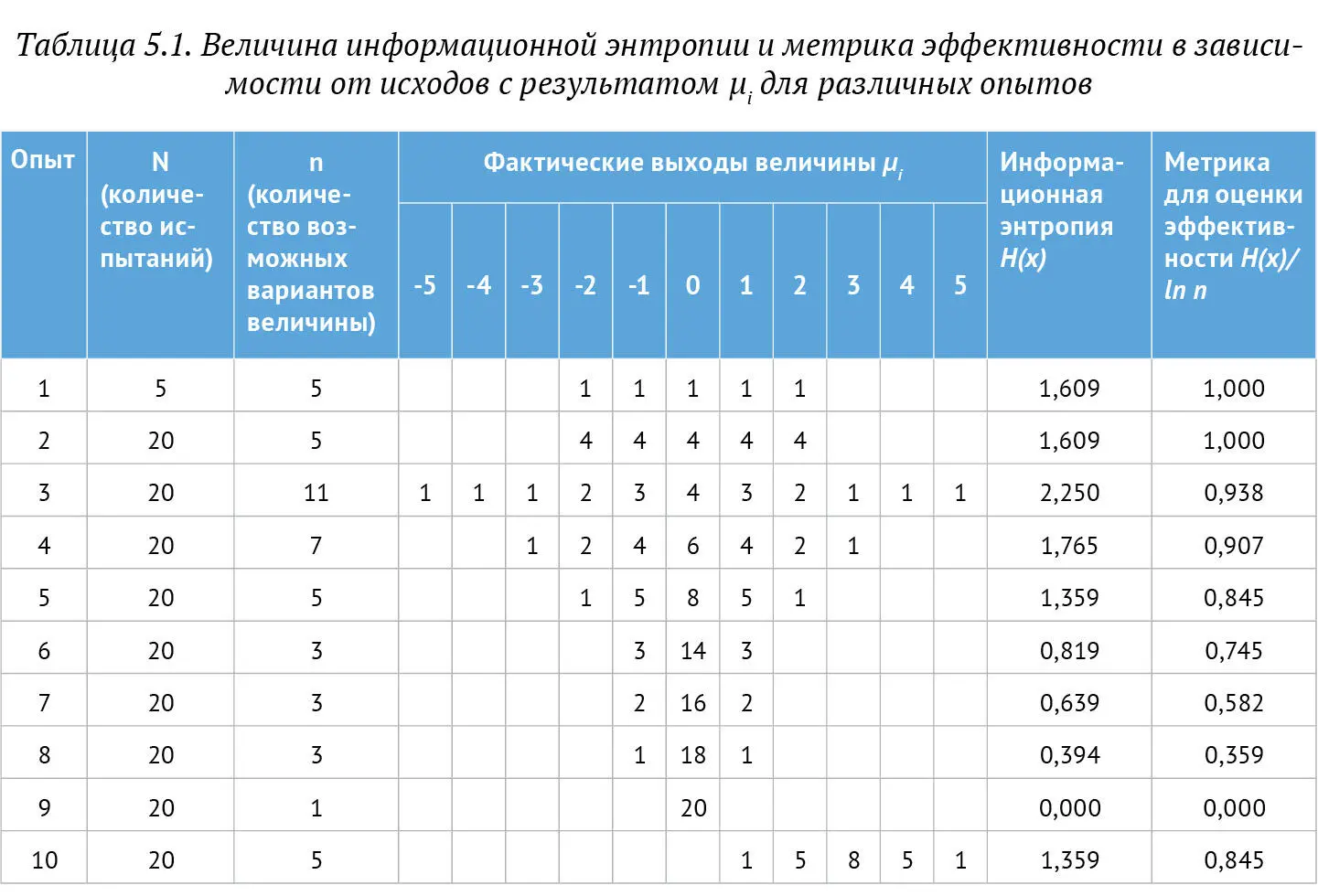
Для равномерно распределенной величины значение введенной метрики равно 1 независимо от количества испытаний (опыты 1 и 2). Из опытов 2–9 очевидно, что с уменьшением количества возможных вариантов, которые может принимать величина n, значение предложенной метрики также уменьшается, что соответствует сокращению неопределенности, связанной с возможными результатами процесса. Также отметим, что предложенная метрика одинакова для смещенных результатов (см. опыты 5 и 10). Это означает, что данная метрика не оценивает «качество» процесса с точки зрения соответствия его результатов некому целевому значению (в отличие от метода «шесть сигма»), а только его неопределенность.
Третье и четвертое свойства энтропии позволяют обобщить предложенную метрику на случай, когда ИС поддерживает одновременно несколько независимых или зависимых бизнес-процессов.
Пример использования энтропийного метода
Читать дальше

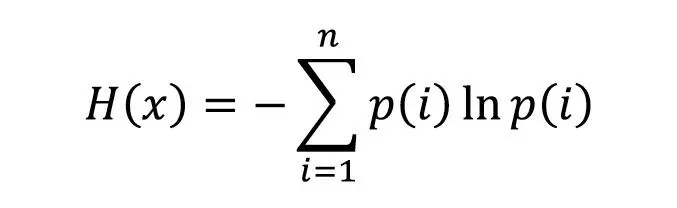
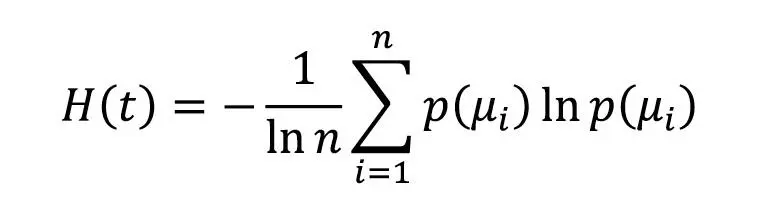
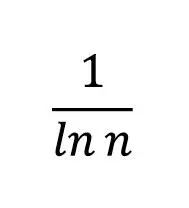 в формулу делает метрику универсальной и позволяет использовать ее как для общей оценки зрелости исследуемого бизнес-процесса (чем ближе его метрика к 0, тем более предсказуемы его исходы), так и даже для сравнения эффективности различных процессов. Для лучшего понимания введенной метрики рассмотрим таблицу 5.1, в строках которой приведено количество исходов с результатом μi для различных опытов.
в формулу делает метрику универсальной и позволяет использовать ее как для общей оценки зрелости исследуемого бизнес-процесса (чем ближе его метрика к 0, тем более предсказуемы его исходы), так и даже для сравнения эффективности различных процессов. Для лучшего понимания введенной метрики рассмотрим таблицу 5.1, в строках которой приведено количество исходов с результатом μi для различных опытов.












