John Crisp - Introduction to Microprocessors and Microcontrollers
Здесь есть возможность читать онлайн «John Crisp - Introduction to Microprocessors and Microcontrollers» весь текст электронной книги совершенно бесплатно (целиком полную версию без сокращений). В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Год выпуска: 2004, ISBN: 2004, Издательство: Elsevier, Жанр: Компьютерное железо, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Introduction to Microprocessors and Microcontrollers
- Автор:
- Издательство:Elsevier
- Жанр:
- Год:2004
- ISBN:0-7506-5989-0
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 60
- 1
- 2
- 3
- 4
- 5
Introduction to Microprocessors and Microcontrollers: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Introduction to Microprocessors and Microcontrollers»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Introduction to Microprocessors and Microcontrollers — читать онлайн бесплатно полную книгу (весь текст) целиком
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Introduction to Microprocessors and Microcontrollers», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
The higher the temperature, the more mobile the electrons, the greater the random voltages and the more electrical noise is present. A solution:
High temperature = high noise
so:
Low temperature = low noise.
Put the whole system into a very cold environment by dropping it in liquid nitrogen (about –200°C) or taking it into space where the ‘shade’ temperature is about –269°C. The cold of space has created very pleasant low noise conditions for the circuits in space like the Hubble telescope. On Earth most microprocessors operate at room temperature. It would be inconvenient, not to mention expensive, to surround all our microprocessor circuits by liquid nitrogen. And even if we did, there is another problem queuing up to take its place.
Let’s return to the Big Match. Two doors finally open and the fans pour through the turnstiles. Now we may expect an equal number of people to pass through the two entrances as shown in Figure 2.8 but in reality this will not happen. Someone will have trouble finding their ticket; friends will wait for each other; cash will be offered instead of a ticket; someone will try to get back out through the gate to reach another section of the stadium. As we can imagine, the streams of people may be equal over an hour but second by second random fluctuations will occur.
Figure 2.8 The fans enter the stadium
Electrons don’t lose their tickets but random effects like temperature, voltage and interactions between adjacent electrons have a very similar effect.
A single current of, say, 1 A can be split into two currents of 0.5 A when measured over the long-term, but when examined carefully, each will contain random fluctuations. This type of electrical noise is called partition noise or partition effect. The overall effect is similar to the thermal noise and, between them, would cause too much noise and hence would rule out the use of a 10-digit system.
The 10-finger system that we use is called a ‘denary’ or ‘decimal’ system. We have seen that a 5 V supply would accommodate a 10-digit counting system if each digit was separated by 0.5 V or, using the more modern choice of 3.3 V, the digits would be separated by only 0.33 V.
Question : Using a 5 V supply and a denary system, what is the highest noise voltage that can be tolerated?
Answer : Each digit is separated by only 5 V/10 = 0.5 V. The number 6 for example would have a value of 3 V and the number 7 would be represented by 3.5 V. If the noise voltage were to increase the 3 V to over 3.25 V, the number is likely to be misread as 7. The highest acceptable noise level would therefore be 0.25 V. This is not very high and errors would be common. If we used a supply voltage of 3.3 V, the situation would get even worse.
So why don’t we just increase the operating voltage to say, 10 V, or 100 V? The higher the supply voltage the less likely it is that electrical noise would be a problem. This is true but the effect of increasing the supply would be to require thicker insulation and would increase the physical size of the microprocessor and reduce its speed. More about this in Chapter 11.
If we reduce the number of digits then a wider voltage range can be used for each value and the errors due to noise are likely to occur less often.
We have chosen to use only two digits, 0 and 1, to provide the maximum degree of reliability. A further improvement is to provide a safety zone between each voltage. Instead of taking our supply voltage of 3.3 V and simply using the lower half to represent the digit 0 and the top half for 1, we allocate only the lower third to 0 and the upper third to 1 as shown in Figure 2.9. This means that the noise level will have to be at least 1.1 V (one-third of 3.3 V) to push a level 0 digit up to the minimum value for a level 1.
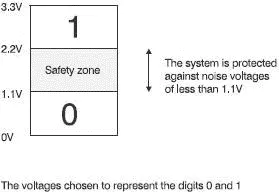
Figure 2.9 A better choice of voltages
Normally, we count in the system we call ‘denary’. We start with 0
then go to 1 then to a new symbol that we write as 2 and call ‘two’. This continues until we run out of symbols. So far, it looks like this:
0
1
2
3
4
5
6
7
8
9
At this point we have used all the symbols once and, to show this, we put a ‘1’ to the left of the numbers as we re-use them. This gives us:
10
11
12
13
14
… and so on up to 19 when we put a 2 on the left-hand side and start again 20, 21, 22 etc.
When we reach 99, we again add a ‘1’ on the left-hand side and put the other digits back to zero to give 100. After we reach 999, we go to 1000 and so on.
Counting is not easy. We often take it for granted but if we think back to our early days at school, it took the teacher over a year before we were happy and reasonably competent. So counting is more difficult than microprocessors – you’ve mastered the difficult part already!
The base of a number system is the number of different symbols used in it. In the case of the denary system, we use 10 different symbols, 0…9, other numbers, like 28 657, are simply combinations of the 10 basic symbols.
Since the denary system uses 10 digits, the system is said to have a base of 10. The base is therefore just the technical word for the number of digits used in any counting system.
We can count using any base that we like. In the denary or decimal system, we used a base of 10 but we have seen that microprocessors use a base of 2 – just the two digits 0 and 1. This is called the binary system.
We usually abbreviate the words BInary digiT to bit. Counting follows the same pattern as we have seen in the denary system: we use up the digits then start again. Let’s give it a try. Start by listing all the digits:
0
1
and that’s it!
We now put a ‘1’ in the next column and start again:
10
11
It is convenient at this stage to keep the number of binary columns the same and so we add a 0 at the start of the first two digits. These extra zeros do not alter the value at all. For example, the denary number 25 is not affected by writing it as 025 or 0025 or even 000 000 000 000 025.
The binary and decimal equivalents are:
| Binary | Denary |
|---|---|
| 00 | 0 |
| 01 | 1 |
| 10 | 2 |
| 11 | 3 |
We do the same again – put a ‘1’ in the next column and repeat the pattern to give:
| Binary | Denary |
|---|---|
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
and once more:
| Binary | Denary |
|---|---|
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
Here is a number: 1000. But what number is it? Is it a thousand in denary or is it eight written in binary?
I don’t know. I could take a guess but the difference between flying an aircraft at eight feet and a thousand feet is a serious matter. The only way to be certain is to say so at the time. This is done by showing the base of the number system being used to make the meaning quite clear. The base of the number system is shown as a subscript after the number.
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Introduction to Microprocessors and Microcontrollers»
Представляем Вашему вниманию похожие книги на «Introduction to Microprocessors and Microcontrollers» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Introduction to Microprocessors and Microcontrollers» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.












