О солнечных и лунных затмениях слышали все, а кто-то и наблюдал их. Для математика это зримые примеры вычитания множеств; взгляните на рис. 84 – чем не затмения? Серую область можно трактовать как результат вычитания одного круга из другого. На левом рисунке белый круг «отгрыз» часть черного, превратив его в серую область, а на правом – наоборот. Подобающие этим случаям формулы будут таковы.
G = B – W или G = W – B

Рис.84 – Вычитание множеств
А если вычитаемый круг окажется больше того, из которого вычитают, и полностью поглотит его? В алгебре разность получится отрицательной, а здесь? Ничего подобного! При вычитании большего множества из меньшего или равного ему получается пустое множество, оно обозначается символом Ø. Из пустого множества тоже можно вычитать, и результатом опять будет пустое множество.
(B – B) – B = Ø
(Ø – W) – B = Ø
Вот такими интересными свойствами обладают множества!
Подмножества и надмножества
На рис. 85 белый круг полностью поглощен черным. Тогда говорят, что множество точек белого круга составляет подмножество точек черного. Или так: множество точек черного круга является надмножеством точек белого. Математик выразит это формулой:
B > W

Рис.85 Надмножество (B) и подмножество (W)
А если круги совпадают и полностью перекрывают друг друга? Тогда говорят, что множества равны, и любое из них является и подмножеством, и надмножеством другого. В общем случае:
если B ≥ W, то B является надмножеством W;
если B ≤ W, то B является подмножеством W.
Числовые множества
Мы рассмотрели несметные множества бесконечно маленьких точек. Но компьютеры ещё не умеют работать с бесконечностями. Так умерим свой аппетит и перейдем к множествам с конечным числом элементов. Поступим так: вместо раскраски кругов расставим на них ряд жирных точек и пронумеруем их числами от 1 до 9 (рис. 86). В ходе последующих опытов нас будут интересовать лишь эти избранные точки (то есть, числа).
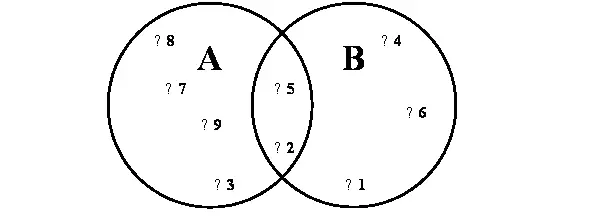
Рис.86 – Множества чисел
Так мы получили два конечных множества чисел. Одно из них, обозначенное буквой A, содержит числа 8, 7, 9, 3, 5, 2. Другое обозначено буквой B и включает числа 5, 4, 6, 1, 2. Эти множества математики записали бы так:
A = { 8, 7, 9, 3, 5, 2 }
B = { 5, 4, 6, 1, 2 }
Для записи множеств они используют фигурные скобки. Обратите внимание: числа в скобках следуют в произвольном порядке. Это значит, что порядок перечисления элементов множества не важен. Учтите также, что числа 2 и 5 входят в оба множества.
Подобно точкам на круге, каждый элемент числового множества уникален, иными словами, может входить в множество лишь единожды. Вспомните нашу попытку покрасить углем черный круг, – добавление к множеству существующих в нём элементов не изменяет его. Этим же свойством обладают и числовые множества. Например, для нашего случая справедливо следующее.
A + { 8, 7 } = A
Множество A после объединения с множеством {8,7} не изменилось, поскольку уже содержало эти числа.
С числовыми множествами поступают так же, как и с бесконечными: объединяют, пересекают, вычитают и сравнивают. Вот примеры этих операций для нашего случая.
Объединение множеств содержит все числа исходных множеств, при этом повторения (дубликаты) отбрасывают:
G = A + B = { 8, 7, 9, 3, 5, 2 } + { 5, 4, 6, 1, 2 } = { 8, 7, 9, 3, 5, 2, 4, 6, 1 }
Хотя числа 2 и 5 входили в оба исходных множества, в объединении они встречаются по разу.
Пересечение множеств содержит только числа, входящие в оба множества:
A * B = { 8, 7, 9, 3, 5, 2 } * { 5, 4, 6, 1, 2 } = { 5, 2 }
Разность множеств A–B содержит числа, состоящие в множестве A, но отсутствующие в множестве B:
A – B = { 8, 7, 9, 3, 5, 2 } – { 5, 4, 6, 1, 2 } = { 8, 7, 9, 3 }
Разность множеств B–A содержит числа, состоящие в множестве B, но отсутствующие в множестве A:
B – A = { 5, 4, 6, 1, 2 } – { 8, 7, 9, 3, 5, 2 } = { 4, 6, 1 }
Эти «вычисления» легко проверить по рис. 86.
Мощность множества, полные и неполные множества
Мощность множества – это наибольшее количество элементов, которое может содержаться в нём. В нашем числовом примере мощность множества равна девяти.
Читать дальше














