Секреты Юлия Цезаря
Римскому полководцу Юлию Цезарю выпали лихие времена. Отправляя гонца с письмом в отдаленный уголок империи, Цезарь рисковал «подарить» свои тайны недругам, – ведь на дорогах было неспокойно. Это надоумило его шифровать свои письма. В чем заключался метод Цезаря?
Прием Юлия состоял в замене одних букв другими путем кругового сдвига алфавита на несколько позиций. На рис. 54 показано превращение букв при сдвиге алфавита на две позиции. Буква «А» становится буквой «В», буква «Б» – буквой «Г» и так далее. Двум последним уготовано превратиться соответственно в буквы «А» и «Б». Такое шифрование превращает письмо в дикую абракадабру!
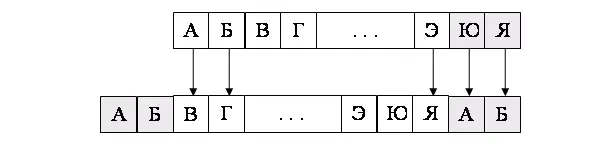
Рис.54 – Принцип шифрования Юлия Цезаря
Как расшифровать её? Очень просто – сдвинуть буквы в обратную сторону. Но надо знать количество сдвигов – это число называют ключом шифра (в примере на рисунке ключ шифра равен двум). Разумеется, что ключ шифра и метод шифрования знали лишь двое: получатель письма и сам Юлий Цезарь.
Пойдем и мы вслед римскому полководцу, – создадим программу для шифрования текстового файла и его расшифровки. Скажу прямо: задача непростая, а потому решать её будем в два этапа. Вначале освоим шифрование отдельной строки, а уж потом «замахнемся» на файл. Но начнем с шифрования отдельного символа.
Суть проблемы
Зашифровать строку – значит зашифровать каждый её символ. Будь у нас готовая функция шифрования символа, задача решалась бы вмиг. Так займемся ею и начнем с заголовка. Дадим нашей функции имя Encrypt – «шифровать», она должна принимать исходный символ и возвращать другой, зашифрованный. Значит, заголовок функции может быть таким:
function Encrypt (X: char): char;
Теперь сосредоточимся на теле функции и рассмотрим известные нам приёмы обработки. Один из них состоит в применении каскада условных операторов:
if X=’А’
then Crypt:=’В’
else if X=’Б’
then Crypt:=’Г’
else...
Насколько удачно это решение? Прикинем количество вложенных операторов в этой лесенке. В русском алфавите 33 буквы, если взять заглавные и строчные, то получится 66. А если надумаем шифровать ещё и латинские буквы, и цифры и знаки препинания, то наберется около двух сотен символов. Такая лесенка условных операторов растянется на несколько этажей!
Не прибегнуть ли к оператору выбора CASE? Тогда тело функции будет намного проще:
case X of
’А’: Crypt:=’В’;
’Б’: Crypt:=’Г’;
...
end;
Обратите внимание, что метками оператора CASE здесь служат символы, – скоро вы узнаете, почему такое возможно. Этот вариант очевидно лучше первого, хотя две сотни меток – тоже не подарок. Но главное неудобство в ином: при изменении ключа шифра придется переписать все ветви оператора CASE, а это, согласитесь, скучно. Не поискать ли иного решения, простого и гибкого?
О кодировании символов
Первые компьютеры принесли инженерам массу неудобств. Взять хотя бы ввод и вывод данных. Дисплеи, принтеры и звуковые карты – тогда никто не слышал о них! Результат размышлений цифрового «мозга» высвечивался лампочками на инженерной панели ЭВМ, и в эту двоичную «цветомузыку» был посвящён лишь узкий круг мудрецов. Со временем изобрели простые принтеры, способные печатать лишь цифры, а затем и более совершенные – для печати букв и других символов. Как действуют подобные устройства?
Процессор компьютера, как известно, оперирует с числами. А людям подавай то текст, то картинку. Как связать одно с другим? Здесь инженеры вспомнили об алфавите. Ведь буквы в нём упорядочены, а значит, каждой букве можно сопоставить число; например, букве «А» – один, «Б» – два и так далее. Такое сопоставление называют кодированием, оно и решает проблему представления символов. Намерившись напечатать некоторый символ, компьютер передает его код на принтер, а уж принтер знает, как поступить с этим числом. При вводе с клавиатуры происходит обратное преобразование: нажатие клавиши заставляет клавиатуру отправить в процессор код соответствующего символа.
Итак, символы внутри компьютера кодируются числами. Мы посчитали, что общее количество букв, цифр и других знаков составляет более двухсот. Инженеры не поскупились и отвели для кодирования символов 256 чисел – от 0 до 255 включительно. Почему именно 256, а не 300 или 500?
Читать дальше












