Решение нашей задачи можно высказать так: «проехать можно, если открыта улица A И открыта улица B». Обратите внимание на выделенный курсивом союз «И». Чтобы превратить это рассуждение в логическое выражение и записать на Паскале, надо лишь перевести союз «И» на английский язык – это будет «AND», а названия улиц заменить логическими переменными A и B. И вот результат такого перевода.
if A and B
then S:=’Поезжай на машине!’
else S:=’Топай пешком!’;
Вместо двух условных операторов остался один. Готовая программа будет такой.
{ P_13_1 – первый маршрут проезда }
var A, B : Boolean; S: string;
begin
{ ввод данных со «спутника» }
Write(’Улица A:’); Readln(S); A:= S=’1’;
Write(’Улица B:’); Readln(S); B:= S=’1’;
{ решение }
if A and B
then S:=’Поезжай на машине!’
else S:=’Топай пешком!’;
Writeln(S); Readln
end.
Испытайте программу при разных сочетаниях входных данных и проверьте, не врёт ли она?
Теперь рассмотрим другой маршрут, здесь попасть в школу можно по любой из двух улиц (рис. 32).

Рис.32 – Схема проезда, второй вариант
Обычным языком молвим так: «проезд возможен, если открыта улица A ИЛИ открыта улица B». Союз « ИЛИ » тоже припасен в Паскале, по-английски он пишется «OR». В этом случае решение будет таким.
if A or B
then S:=’Поезжай на машине!’
else S:=’Топай пешком!’;
А вот маршрут на рис. 33 более замысловат.
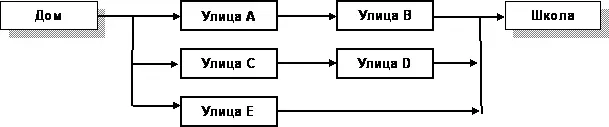
Рис.33 – Схема проезда, третий вариант
Слабо ли вам выразить решение для этого случая? Сказать на обычном языке легко: «проехать можно, если открыта A И открыта B ИЛИ открыта C И открыта D ИЛИ открыта E». Слово «улица» я пропустил. Все, решение готово! Осталось лишь перевести его на язык Паскаль.
if A and B or C and D or E
then S:=’Поезжай на машине!’
else S:=’Топай пешком!’;
Как просто! Здесь опять выделено курсивом логическое выражение. Только теперь оно составлено из булевых переменных и булевых операций AND (И) и OR (ИЛИ). Иногда эти операции называют логическим умножением и логическим сложением. Сходство с арифметикой здесь в том, что каждая логическая операция обладает в выражении своим старшинством: умножение AND выполняется раньше сложения OR. Когда эту последовательность надо изменить, применяют скобки. Пример такого рода показан на рис. 34 (перекресток).

Рис.34 – Схема проезда, четвертый вариант
Сначала скажем словами: «проехать можно, если открыта A ИЛИ открыта B И открыта C ИЛИ открыта D». Переведя на Паскаль буквально, без скобок, получим:
if A or B and C or D
then S:=’Поезжай на машине!’
else S:=’Топай пешком!’;
Поскольку логическое умножение выполняется раньше сложения, Паскаль поймет это так: A or (B and C) or D. Но это не то, что мы хотели! Правильно будет записать наше решение со скобками:
if (A or B) and (C or D)
then S:=’Поезжай на машине!’
else S:=’Топай пешком!’;
Наконец, рассмотрим маршрут на рис. 35, где путь преграждает шлагбаум. Договоримся, что закрытому шлагбауму соответствует значение TRUE (то есть, в сравнении с улицами тут все наоборот).
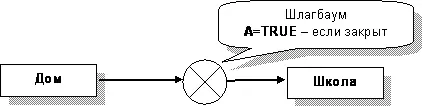
Рис.35 – Схема проезда, пятый вариант
Рассуждая как обычно, скажем так: «проезд возможен, если НЕ закрыт шлагбаум». Здесь применено логическое отрицание НЕ , что по английски значит «NOT». Решение на Паскале будет таким.
if not A
then S:=’Поезжай на машине!’
else S:=’Топай пешком!’;
В отличие от двух предыдущих операций, логическое отрицание – одноместная операция, ей нужен лишь один операнд. Логическое отрицание имеет наивысший приоритет, и выполняется раньше логического умножения и сложения.
Парад логических операций
Итак, посредством логических операций мы переводим рассуждения с человеческого языка на формальный язык программирования, получая при этом логические (булевы) выражения. Логические данные в Паскале можно сравнивать и выполнять с ними четыре логические операции, три из которых вам уже знакомы. Рассмотрим свойства этих операций.
Читать дальше















