Alexander Berlin - Mathematics of the market. Problem book

Not purchased the product can be not offer, for example, to destroy – it named obvious losses.This type market are named a system with obvious losses.

Distribution system can put the product to the queue of waiting for the realization (for the accumulation and, storage of products). This type market is named a system with waiting.

In this case it is important to know the waiting time. It may exceed a reasonable time (the assigned waiting time). In this case we speak of conditional losses. Since the goods available for sale and after a certain time is removed from storage in accordance with agreed terms and conditions.

If the share of refusals of the goods received exceeds a certain number, it indicates overproduction, and requires measures to eliminate such losses.

In order to apply the methods of Queuing theory to the calculation of the basic economic processes, it is necessary to solve one of the key issues of the economy – to determine the product unit measures supply and demand (A-relative consumption).

Let’s start with a quote of Keynes [3.1].

“The difficulties that most bothered me at process writing this book, and I couldn’t clearly articulate their thoughts;

first, the choice of units measurements, suitable for research of economic system as a whole;…”.

“That the units, in terms of which economists commonly work, are unsatisfactory can be illustrated by the concepts of the national dividend, the stock of real capital and the general price-level:”

“The community’s output of goods and services is a non-homogeneous complex which cannot be measured, strictly speaking, except in certain special cases, as for example when all the items of one output are included in the same proportions in another output”.

We will try to find an indicator of demand. Let’s call it the relative consumption. – A Relative

He can to acquire the following extreme values.

If the consumer has satisfied his need for this product, P Relative =1,

If the consumer is just starting to buy a goods P Relative l=0.

Let’s is use your experience.

Do you love cakes? I will sell them to you. You will buy them and will desire buy more. I’m going to sell more and more. Finally, you will begin to eat 10 cakes a day. And I offer you still. You say, “Enough!”

I suggest to You free of charge for 12 cakes a day, and You ungrateful saying “No!”. Moreover, buying cakes, You will some time to consume them, and not buy a new one.

What is it? It is the overproduction!

So the current state of the user can be reflected by the value of the relative consumption

0 ≤ P reliative ≤ 1

Let’s continue the search for the mathematical determination of relative consumption.

Introduce the unit (let’s call it a) that will allow us to measure supply and demand “relative consumption”.

It is the ratio of real consumption A real to the maximum possible A max

It will ratio

A relative. = A real/ A max.= a

For most of the considering cases we can assume that prices A realand A maxare equal so the relative consumption is a dimensionless quantity.

When determining the maximum consumption, we assume that no material (money, prices) and external factors (season, fashion) do not limit the consumer. Then the maximum consumption in a given period will be equal to A max.

Maximum consumption can be standardized (for example, by analogy with the consumer basket). However, it should be noted that the maximum consumption may change in time.

For example, the maximum demand for the commodity “money” may increase depending on the achievements or expectations (the promotion) of technological progress.

The actual and maximum consumption expressed in units of the product (pieces, packages, units of money).

If we use this unit we will for measure the demand and supply of goods, by one consumer or one group of consumers, then we will call this index – SPECIFIC WEIGHT RELATIVE CONSUMPTION and we will denote it a.

If we considered the consumption of a group of n consumers (consumer groups), applied the name RELATIVE CONSUMPTION

A relative= a×n.

In detail, the influence of the processes of functioning of the market for relative consumption (objective, subjective factors, price) considered in [3.1 – 3.3].

In this Chapter we consider methods for calculating throughput of market with full accessibility in the system with obvious losses.

We will consider a simplified mathematical model shown in Fig.2.1.

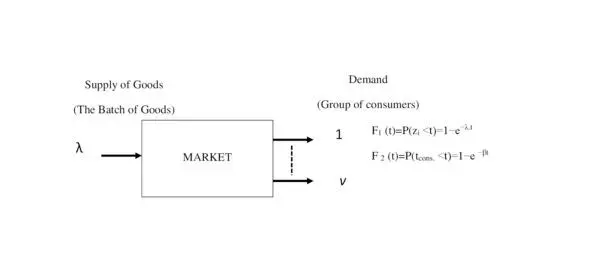
Fig.2.1. Model of the market as a system with obvious losses

In this model, is considered

– the incoming flow of goods, from the system of production

– the flow then enters the distribution system.

– which delivers it into the system of consumption.

The main assumptions which allow to mathematically investigating this process.

Incoming flow:

– consists of identical goods, (this property is named ordinariness)

– result processing of the goods in this moment time does not depend on the results of previous processing (this property is named stationary);

– follow processing of goods the does not depend on the results of previous processing (this property is named the lack of aftereffect).

Random flow, which has all three properties, is called the simplest and well-studied in mass service theory [2.1, 2.2, and 4.3].

The market distribution system

It is assumed that this system has no any stimulating or limiting effect on the service process goods

The system of consumptionoperates as follows.

The system consists of n groups (or individual) consumers.

Each group receiving a certain amount of goods and after out some time (time of consumption – t consum) and may be free for further consumption.

For example, a consumer who bought a vehicle, uses it (consumes) for about 3 years, and then begins to look for a new one.

Not to be confused with the time of consumption and time of possession. User has

the old car, but as soon as he begins to look for a new one car – this point is the end point of consumption.

If satisfied demands one of a group of consumption then the number of groups decreases by one, i.e., for consumption remains n-1 group.

At high intensity can be that there will come a time when all n groups of customers will busy.

Whereupon, the received goods will not be sold. Unsold merchandise we will call a LOSSES.

The probability of losses of the goods with a certain number of receipts and number of groups consumption, can give answer one or more questions.

For example,

1. At what size supply, losses will exceed a given norm?

2. What number of goods can processing the market in a given time?

3. How much should be consumer groups to ensure that given quantities of goods were sold with losses less than or equal to the specified norm?

4. What happens to losses if we increase the supply at a certain value? The appearance on the market of new suppliers or an increase in the supply of production.

The answers to these questions can be found by applying the formula of Erlang.