Валентин Арьков - Статистический анализ взаимосвязи. Учебное пособие

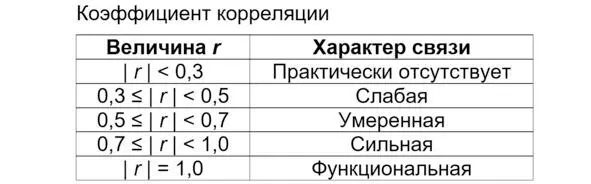
Коэффициент корреляции принимает значения от —1 до +1 включительно.

Знак коэффициента указывает на НАПРАВЛЕНИЕ связи – прямую или обратную связь. Положительная корреляция означает, что с увеличением фактора в среднем возрастает результативный признак. Это прямая связь. Отрицательная корреляция – это обратное направление связи, то есть снижение, убывание, падение графика. С увеличением фактора убывает результат.

Величина (модуль, абсолютное значение) коэффициента характеризует ТЕСНОТУ линейной связи. Чем ближе значение к единице, тем меньше разброс, тем ближе точки к прямой линии. Чем ближе коэффициент к нулю, тем сильнее разброс вокруг прямой. Традиционное толкование величины коэффициента корреляции приводится в таблице.

Возможна и другая ситуация – НЕЛИНЕЙНАЯ зависимость, которая тоже представляет собой отсутствие линейной связи. Нелинейной зависимостью является всё, что не является линейным, например, кривая или ломаная линия. В этом случае коэффициент линейной корреляции будет близок к нулю. Но при этом точки могут быть очень тесно расположены вокруг кривой или ломаной линии. Для анализа степени нелинейной связи используют другие коэффициенты корреляции. В данной работе мы ограничимся только анализом тесноты линейной зависимости.

Как и во многих других случаях, для вычисления коэффициента корреляции в Excel имеются несколько способов:

– надстройка;

– функции;

– формулы.

В следующих разделах мы рассмотрим все эти возможности, а затем сравним полученные результаты.

Вызываем модуль Корреляциястатистической надстройки:

Data – Analysis – Data Analysis – Correlation

Данные – Анализ – Анализ данных – Корреляция.

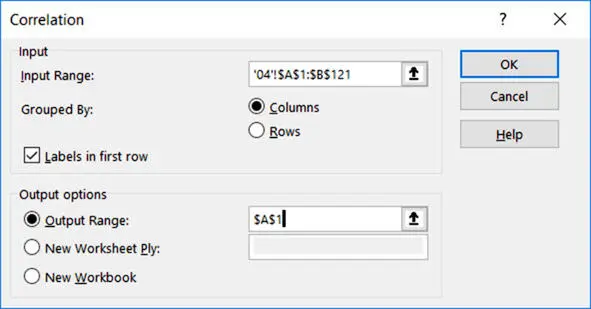
Параметры корреляционного анализа

В диалоговом окне

Correlation

Корреляция

указываем следующие параметры:

Input – Input Range

Входные данные – Входной интервал.

В выбранном диапазоне ячеек должны быть два столбца значений Xи Y.

Затем указываем расположение исходных данных:

Labels in first row

Метки в первой строке.

Выделяем значения в столбцах Xи Yвместе с их заголовками. В этом случае в таблице с результатами анализа будут выводиться названия переменных.

Указываем, что наши исходные данные расположены по столбцам:

Grouped By – Columns

Группирование – по столбцам.

Обратите внимание, что здесь имеется в виду расположение данных по столбцам, а не статистическая группировка, хотя на экране и присутствует слово ГРУППИРОВАНИЕ. Как говорил Козьма Прутков: «Не верьте глазам своим». Мы пока что просто описываем исходные данные и даже не начинали заниматься группировкой.

Отмечаем первую ячейку, начиная с которой будут выводиться результаты анализа:

Output options – Output Range

Параметры вывода – Выходной интервал.

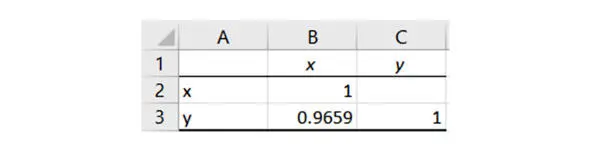
Результаты корреляционного анализа

На экран выводится таблица коэффициентов корреляции. На пересечении строки Yи столбца Хвыводится искомый коэффициент. Единичные коэффициенты на диагонали – это корреляция переменной с самóй собой.

Чтобы получить больше разрядов в дробной части, увеличим ширину столбца.

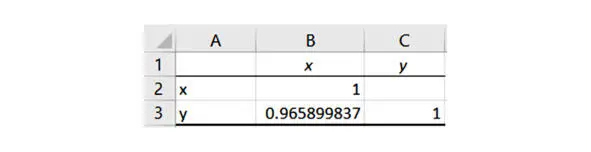
Точное значение коэффициента

Второй способ вычисления коэффициента корреляции – это готовая функция

CORREL (array1, array2)

КОРРЕЛ (диапазон_x; диапазон_y).

Два обязательных аргумента – это диапазоны ячеек Xи Y. Здесь «иксы» и «игреки» задаются по отдельности. Напомним, что в английской версии программы аргументы функции разделяют запятой, а в русской – точкой с запятой.

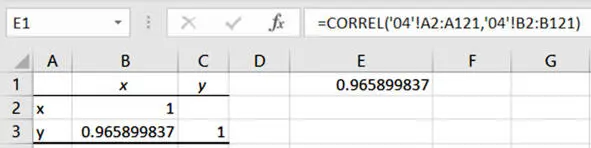
Вызов функции CORREL