Сергей Толкачев - Активные данные. Философское программирование

Слово делать относится как раз к такой категории интуитивно понятных, и положительный ответ на вопрос «Может ли машина делать?» , особенно если речь идет о физических действиях, не должен вызвать каких-либо сомнений (разве что филологических). Но и у программистов не видно серьезных оснований для возражений по поводу способности информационных машин – ведь стоит загрузить программу в компьютер, как в нем начинаются действия. Как в физике, так и в информатике, действие всегда приводит к изменению состояния, и это изменение в энергетической машине может быть измерено в джоулях, а в информационной – в битах. Мы не будем здесь углубляться в сравнение свойств физических и информационных систем, например закона сохранения энергии с его информационным аналогом, или определения работы в физических и информационных системах. Однако если эта тема заинтересует любопытного читателя, то можно быть уверенным, что его ждут интересные и неожиданные открытия.

Но ведь и человек способен к делу , равно как и множество живых существ, которые тоже совершают самые разнообразные осмысленные, и не очень, действия. Почему бы не расширить класс машин , добавив к нему биологические системы? При этом у нас появляется возможность изучить связи между информационными действиями и соответствующими физиологическими реакциями, на целом спектре разнообразных организмов, поскольку биологическая эволюция предоставила нам последовательный ряд: от примитивного червяка-нематоды C. еlegans , до человека разумного, в которых связи между информационными и физическими органами уже достаточно хорошо изучены и описаны.

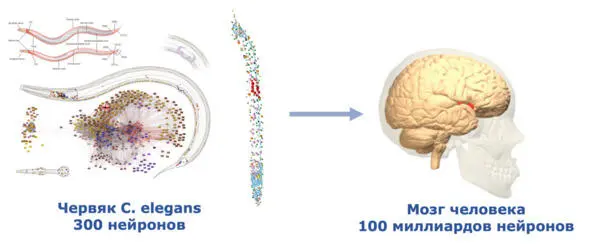
Если сравнить рефлекторные реакции в ответ на возбуждения в простейших организмах, с тем, как анализирует вопросы и генерирует ответы человек в процессе диалога, то можно проследить, как видоизменяются биологические системы, созданные с применением одного и того же базового конструктивного элемента – нейрона. Правда, проводить измерения внутри живых организмов дело тонкое и вряд ли в скором времени мы сможем создать универсальную структурно-функциональную модель, в которой для каждого органа будут получены энерго-информационные характеристики в джоулях и битах. Но характерные особенности и отличия в структурах различных по сложности организмов, могут дать хорошую пищу для рассуждений.

А «Может ли машина мыслить?» – с этого вопроса начинается, одна из самых популярных в истории вычислительной техники, статья А. Тьюринга «Вычислительные машины и разум». Этот вопрос вызвал бесконечное количество дискуссий и безусловно до сих пор, он является одним из самых интересных теоретических вызовов для многих программистов, и не только. Но если сформулировать его несколько иначе – «Как машина может помочь человеку мыслить?» , то из области сложных формальных проблем, с которыми столкнулся Тьюринг и его последователи, мы переходим к инженерным системам и техническим определениям, где результат должен быть конкретен и может быть измерен понятным способом, например, как КПД физической машины, заменяющей ручной труд человека.

На первый взгляд, такая игра словами может показаться простой забавой для ума, однако, когда Тьюринг попытался найти формальный подход к ответу на свой вопрос, он тоже решил переформулировать его в других, менее двусмысленных терминах, и назвал эту проблему – « играв имитацию ». В результате появился хрестоматийный « тест Тьюринга », который пытаются пройти поколения программистов. Если бы только Тьюринг смог предвидеть, что слово имитация в будущем, будет многими воспринято буквально и безотносительно к слову игра , то кто знает, возможно он попробовал бы подобрать ещё более аккуратные термины, и тогда, мы бы имели больше полезных функциональных чат-ботов, вместо множества «имитаторов», способных поддерживать лишь разговоры на общие темы.

Знаменитый вопрос Тьюринга можно рассматривать как продолжение его другой, не менее знаменитой, концепции универсальной вычислительной машины, которую он предложил в 1936 году. Для математиков машина Тьюринга, это несомненно прорыв, поскольку, согласно А. Черчу, Тьюринг – первый, кто ввел физическое действие в математическое понятие вычисления. В математике, с момента её возникновения, существует разрыв между «строго формальной» абстрактной теорией, и интерпретатором этой теории, которым всегда выступает другой математик. И каким бы строгим не было доказательство, в конце концов, проверяет его человек. У математиков нет компилятора, который является обыденным инструментом для программистов, а Тьюринг, если уж совсем упрощенно, предложил и обосновал возможность такого математического компилятора, по крайней мере, для вычислительных задач. Впрочем, при всей важности машины Тьюринга для фундаментальных исследований, программируют на ней лишь редкие математики и студенты курса «Теоретическое программирование», и вряд ли на всей Земле можно найти программиста, который использует её для решения своих практических задач.