Александр Блинков - Переизобретение бизнесов. Физика и технология

Анри Пуанкаре (1854—1912), «последний из величайших математиков-универсалов», также говорил, что в деле понимания качественных изменений в поведении систем необходим лишь ограниченный объем информации качественного характера.

Итак, формул не будет. Они бесполезны. Но есть хорошая новость! Оказывается, важно не высчитать точную траекторию изменений, а быть готовым к явлению – к критической точке и к качественному переходу, который за этим последует. Собственно, так мы и поступаем утром, когда кипятим воду для чая. Мы ничего не вычисляем и не измеряем, мы просто ждем момента качественного перехода – ждем закипания воды. И нам этого оказывается достаточно, чтобы понять – момент наступил, можно заваривать чай.

Вернемся к нашей резинке, к нашей ручной бифуркации. Когда мы сжали ее и получили прогиб, можем поиграться с ней дальше, например, попробовать давить на место выпуклости.

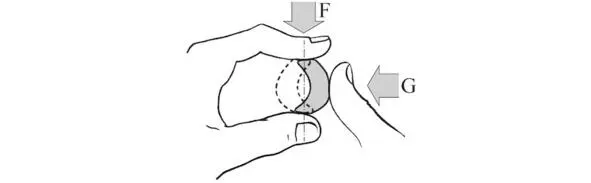
Рис. 6. Продольное и поперечное воздействие на упругий объект

Наш «антистресс» при определенном усилии начнет перещелкиваться в противоположную сторону. Если мы нарисуем множество решений уравнения в пространстве параметров: Прогиб/Давление продольное/Давление поперечное, то обнаружим в нем забавную поверхность, похожую на сборку ткани. Эта поверхность в разделе математики под названием Теория катастроф и называется Катастрофа Сборки.

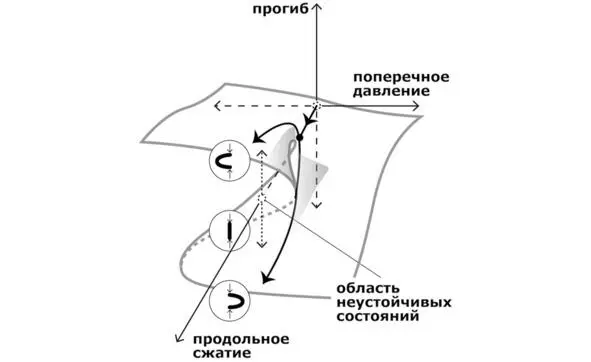
Рис. 7. Поверхность состояния упругого объекта. Выпучивание при продольном сжатии

На этой поверхности решений мы увидим маршрут с выпучиванием при продольном давлении, который мы уже видели на рис. 5. Для этого достаточно рассечь нашу Сборку вертикальной плоскостью, для которой поперечное давление равно нулю.

Область неустойчивости представлена треугольным «язычком», обозначена пунктиром в середине складки, куда система может попасть и какое-то время пробыть в таком состоянии, пока любое бесконечно малое воздействие не выбросит ее в одну из зон устойчивости – прогиб в одну или другую сторону.

Мы также можем проследить траекторию состояния объекта под воздействием поперечного давления.

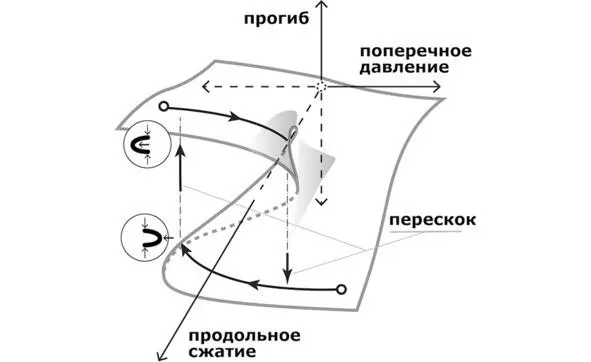
Рис. 8. Поперечный маршрут на поверхности состояния. Эффект памяти

Само по себе понимание математической катастрофы, как качественной картинки пространства возможных состояний, уже позволяет нам много понять в поведении объекта, быть готовым к неожиданностям и более того – использовать эти свойства.

Поперечный маршрут – перебрасывание подобных систем из одного состояния в противоположное (так называемое, явление гистерезиса) используется много где, например, в ячейках бинарной памяти. И чтобы использовать эту память, оказывается надо контролировать только один управляющий параметр, который и переключает ячейку.

За границами физики как точной науки, возникают попытки обобщить образование и самоорганизацию структур в открытых системах, далеких от термодинамического равновесия. По замыслу своего создателя профессора Германа Хакена, синергетика – это междисциплинарное направление, которое призвано играть роль своего рода метанауки, подмечающей и изучающей общий характер тех закономерностей и зависимостей, которые частные науки считали «своими».

«Синергетика (от др. греч. приставки «син» со значением совместности и «эргон» – деятельность) – «вместедействие».

«Следует подчеркнуть, что синергетика отнюдь не является одной из пограничных наук типа физической химии или математической биологии, возникающих на стыке двух наук.»

Это достаточно новое направление наук – еще нет ни четких границ, ни даже четких определений областям. Область исследований синергетики четко не определена и вряд ли может быть ограничена, так как ее интересы распространяются на все отрасли естествознания. Общим признаком является рассмотрение динамики любых необратимых процессов и возникновения принципиальных новаций.

Раз нет четких границ и определений – наблюдается неизбежный в научных и околонаучных кругах спор. Любой готов объявить себя ревнителем истинного метазнания, а всех остальных окрестить псевдоучеными, схоластами и шарлатанами.