Александр Блинков - Переизобретение бизнесов. Физика и технология

Как бы «пощупать» эту самую бифуркацию? Поиграть с ней, посмотреть на эту странную само-организацию . Это, оказывается, не сложно – бифуркации с нами и вокруг нас в большом количестве!

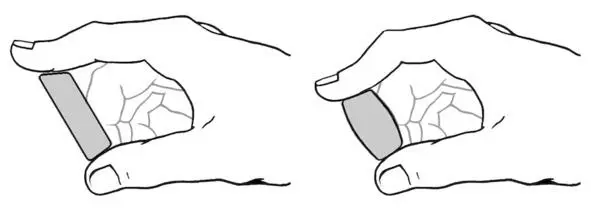
Рис. 3. Ожидаемое поведение упругого объекта

Вряд ли в сегодняшнем компьютерном мире кто-то использует ластик – резинку для стирания написанного карандашом или ручкой. Может быть, вы помните этот предмет еще со школы? Такой маленький кирпичик резинки, которым было забавно играться, сжимая его пальцами. А сейчас, давайте, извлечем науку из такого «антистресса» нашего детства.

Сжимая резинку между пальцами, мы делаем ее короче. Сжимаем еще сильнее – еще сильнее деформируем упругий брусок.

Но в какой-то момент резинка внезапно отказывается дальше сжиматься и выгибается в сторону. Сжимая и разжимая пальцы, мы раз за разом достигаем этой точки, когда поведение простого упругого объекта качественно меняется. Причем каждый раз по-разному: когда-то прогиб будет в одну сторону, а когда-то – в другую.

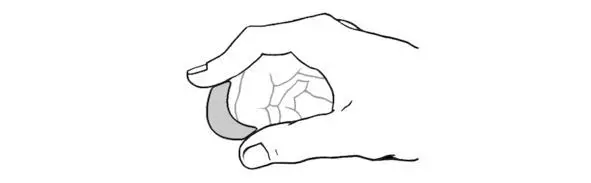
Рис. 4. Выпучивание – реальное поведение упругого объекта

Уравнение, как мы и обещали, писать не будем, лишь скажем, что оно имеет однозначное решение только до определенного сжатия. И в этой критической точке – решение теряет устойчивость . Если представить, что у нас абсолютно идеальный внутри и снаружи брусок резинки, и мы строго вдоль ее продольной оси нажимаем пальцами – резинка будет сжиматься и дальше без выпучивания. Но это будет уже неустойчивым участком решений . Подобно тому, как шарик может в принципе держаться на верхушке выпуклой поверхности, но только в абсолютно идеальном случае.

Если хотя бы чуть-чуть «пошевелить» пальцем – физически, или параметром однородности нашей резинки – математически, решение уравнения равновесия тут же устремится к другому, устойчивому состоянию. Но! Теперь в решении оказывается два возможных устойчивых состояния – прогиб либо «вправо», либо «влево», и в какое именно попадет наш объект зависит от тех самых случайных, буквально микроскопических «шевелений».

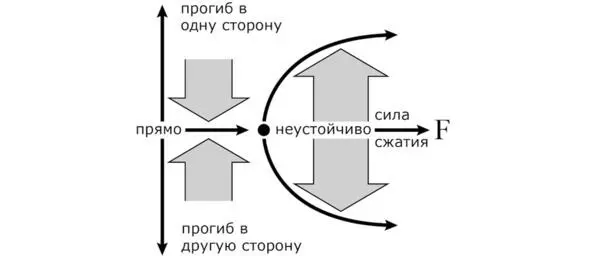
Рис. 5. Состояние резинки под давлением

То есть дело не в том, что мы не умеем считать, а в том, что математика принципиально не может дать однозначного решения. Наоборот, математика доказывает, что теперь однозначности и быть не может! Более того, если бы мы взяли не резиновый брусочек, а резиновый цилиндрик – возможных положений после прогиба мы бы получили не два, а бесконечное количество – любое направление по кругу.

Подытожим, в какое состояние система перейдет, попав в критическую точку, математики не могут однозначно посчитать – решения становятся неустойчивыми относительно флюктуаций . Это означает, что решения уравнений есть, но их может быть много. И даже бесконечно много. Какое решение реализуется на практике – зависит от бесконечно малых отклонений в параметрах, которые возникают только в реальном мире, точнее – в микромире, и которые человек и, следовательно, математика не могут знать никогда. Это такие малые движения, такие малые неоднородности материала резинки, которые невозможно ни измерить, ни запланировать, ни учесть заранее. Такие малые отклонения – это и есть флюктуации . Чтобы рассчитать точное состояние сложной системы в будущем, требуется на берегу знать огромное множество начальных условий, которые никогда никому не будут известны. И уж кто-кто, а бизнес – это точно система с бесконечным количеством неопределенности.

Итак, похоже, мы у разбитого корыта?

Однако послушаем великих. Кажется, не все так безнадежно!

Математика описания нелинейных эффектов весьма нетривиальна. Но, как сказал один из крупнейших математиков XX века академик В. И. Арнольд (1937—2010): «С этими объективными законами функционирования нелинейных систем нельзя не считаться. Выше сформулированы лишь простейшие качественные выводы. Теория доставляет также количественные модели, но качественные выводы представляются более важными и в то же время более надежными: они мало зависят от деталей функционирования системы, устройство которой и численные параметры могут быть недостаточно известными.»