Елена Гариани - Когда поют руны

Двенадцать рун имеют два наклонных реза

Семь рун имеют три и более наклонных реза

Структура рун в числовом виде

4+(5+5)+(6+6)+7=33

А ещё каждой руне соответстует своё число. Кот показал мне два варианта классификации числового ряда простых чисел.

Вариант I

Числовой ряд от 1 до 33

1. Простые числа – целые числа, больше 1, которые имеют лишь два положительных делителя: 1 и само это число.

этих чисел 12

1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31

2. Числа, имеющие два сомножителя

этих чисел 10

6=2*3, 10=2*5, 14=2*7, 22=2*11, 26=2*13

9=3*3, 15=3*5, 21=3*7, 25=5*5, 33= 3*11

3. Числа, имеющие более двух сомножителей

этих чисел 7

12=2*2*3, 18=2*3*3, 20=2*2*5, 24=2*2*2*3, 27=3*3*3, 28=2*2*7, 30=2*3*5

4. Числа, имеющие в качестве своих множителей только 2

этих чисел 4

4=2*2, 8=2*2*2, 16=2*2*2*2, 32=2*2*2*2*2

Структура числового ряда от 1до 33

4+(5+5)+(6+6)+7=33

Вариант II

Числовой ряд от 3 до 35

1. Простые числа – целые числа, больше 1, которые имеют лишь два положительных делителя:

этих чисел 10

3, 5, 7, 11, 13, 17, 19, 23, 29, 31

2. Числа, имеющие два сомножителя

этих чисел 12

6=2*3, 10=2*5, 14=2*7, 22=2*11, 26=2*13, 34=2*17

9=3*3, 15=3*5, 21=3*7, 25=5*5, 33= 3*11, 35=5*7

3. Числа, имеющие более двух сомножителей

этих чисел 7

12=2*2*3, 18=2*3*3, 20=2*2*5, 24=2*2*2*3, 27=3*3*3, 28=2*2*7, 30=2*3*5

4. Числа, имеющие в качестве своих множителей только 2

этих чисел 4

4=2*2, 8=2*2*2, 16=2*2*2*2, 32=2*2*2*2*2

Структура числового ряда от 3до 35

4+10+(6+6)+7=33

– И какой из вариантов правильный?

– Ты живёшь в дуальном мире. Есть ЛЕВО, но есть и ПРАВО. Можно вращаться волчку в одну сторону, а можно и в другую. Есть этот мир, а есть и иной…

– Ого! И какой вариант правильный?

– Ищи ответ сама.

За окном уже мерцала темнота. Кот вернулся к своей игре. Я немилосердно устала и писать каждую строчку становилось всё трудней.

– О чём спел тебе Сфинкс? – не поворачивая головы, спросил вдруг Кот.

Я усиленно думала, но ничего не вспоминалось, кроме ночной тишины в пустыне вокруг Сфинкса – ох уж этот Кот с его иносказаниями!

И пообещала себе накопать в интернете всё, что есть о Сфинксе.

* * *

С утра я проспала, поэтому толком не позавтракала и до остановки маршрутки почти всю дорогу бежала. На работе «слетела» один-эска. Мы с Васильевной в ожидании специалиста из «Гэндальфа» разгоняли утреннюю дрёму крепким чаем. Я слушала болтовню главбуха, кивала и поддакивала в нужных местах.

Фикусы на подоконнике довольно купались в утренних лучах солнца. А за окном небольшой город жил своей повседневной жизнью: куда-то спешили люди, ехали машины и автобусы, высоко над городской суетой неторопливо плыли пушистые облака.

Васильевна была недовольна новой девушкой своего старшего сына: она была старше и у неё был ребёнок.

– Она всё время требует денег! Он дал ей пять тысяч на коммунальные, а она два новых платья купила!

Я молча кивнула. Мамы всегда любят своих детей, иногда слишком любят… Сыну Васильевны шёл тридцать восьмой год, но она по-прежнему опекала и заботилась…

– Ну что?! Ну что он должен ей сказать?! – опять патетически ворвался в мои думы громкий голос главбуха.

Мыслями я была далеко от один-эски, фикусов и старшего сына Васильевны. Я снова вспоминала лицо спасшего меня парня, выхваченное из темноты огнём, и ещё одно – выразительный женский профиль, проявленный из камня неизвестным мастером.

Рядом со Сфинксом не было пирамид! Это была первая загадка.

Дальше в дело вступил интернет. Вокруг гигантской статуи витала уйма загадок. Много спорили о времени появления и о тайных ходах под землёй.

* * *

– И? Что нашла?

Кот терпеливо слушает, но оживляется только когда речь заходит о пропорциях, которые использованы при постройке Сфинкса. В его пропорции заложены десять отрезков золотого сечения!

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

Геометрическое изображение золотой пропорции:

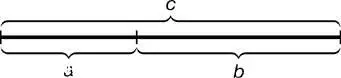
a : b = b : c или с : b = b : а